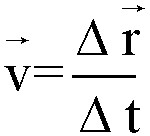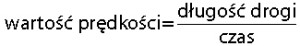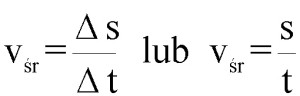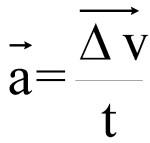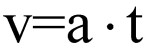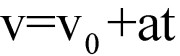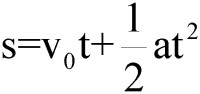Czym jest kinematyka?
Ten dział fizyki zajmuje się opisem ruchu ciał w najprostszym możliwym aspekcie. Na nim bazuje wiele sytuacji, z jakimi mamy do czynienia na co dzień, na przykład podczas jazdy samochodem.
Aby jakaś teoria była kompletna, trzeba przedstawić zbiór założeń. Bez nich, nie wiadomo, kiedy można ją stosować i jakie ma ograniczenia.
Założenia
Pomijane są gabaryty obserwowanych obiektów, ich masa oraz działające na nie siły. Najczęściej traktujemy ciała fizyczne jako nieskończenie małe punkty.
Kinematyka należy do mechaniki klasycznej, czyli nie są uwzględniane efekty relatywistyczne, wynikające z Ogólnej Teorii Względności oraz Szczególnej Teorii Względności, sformułowanych na początku XX wieku.
Zatem trzeba przyjąć, że szybkość analizowanych obiektów jest znacznie mniejsza od szybkości światła, aby efekty relatywistyczne można było pominąć. Jeżeli jest inaczej, trzeba odwołać się do bardziej złożonych wzorów, uwzględniających te efekty, aby wyniki były dokładne.
Kto ją stworzył?
Mechanika klasyczna (i należąca do niej kinematyka) bazuje na zasadach sformułowanych i opisanych przez Isaaca Newtona. Ten uczony żył na przełomie XVII i XVIII wieku, a mimo tego wiele z opisanych przez niego zasad ma zastosowanie również dzisiaj.
Newton był autorem również wielu innych opracowań - na przykład, sformułował prawo powszechnego ciążenia (czyli opisał grawitację), jak również znacznie przyczynił się do rozwoju rachunku różniczkowego, który dzisiaj jest podstawą opisu obiektów w fizyce. Miał dokonania również w innych dziedzinach, na przykład w astronomii.
Podstawowe pojęcia
Aby sprawnie posługiwać się zbiorem zasad, trzeba znać zastosowany w nich słownik. Bez niego można dojść do błędnych wniosków. Każde pojęcie w fizyce ma ściśle określone znaczenie i do stosowania synonimów trzeba podchodzić ze znaczną ostrożnością. To jest cecha charakterystyczna dla każdej nauki ścisłej.
Układ odniesienia
Bez niego nie mielibyśmy pojęcia, czy obiekt w ogóle się przemieszcza. Układem odniesienia jest zazwyczaj układ współrzędnych. Jego stopień złożoności (liczba wymiarów) jest zależna od tego, w jaki sposób chcemy opisać ruch ciała:
- po linii prostej wystarczy jedna współrzędna (na osi X)
- po płaszczyźnie potrzebne są dwie współrzędne (X i Y)
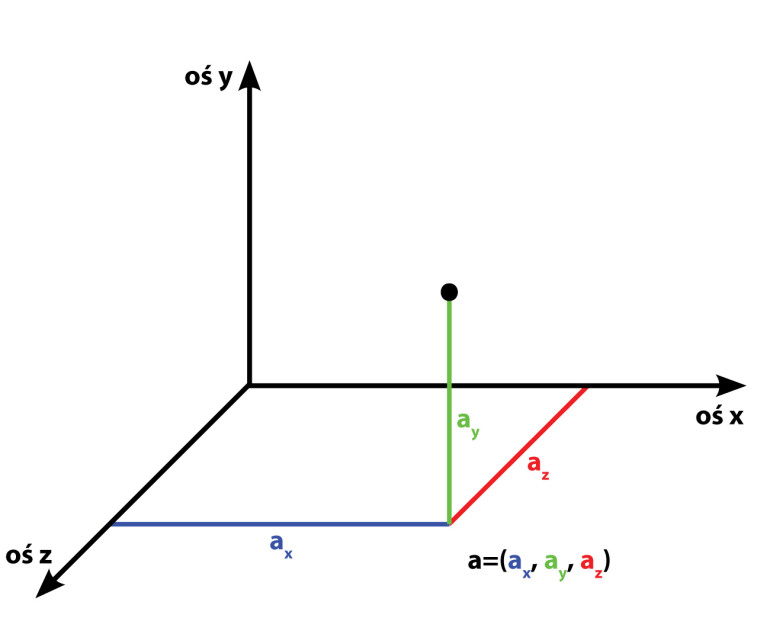
- w przestrzeni wymaga już trzech współrzędnych, na osiach X, Y i Z.
Na przykład tocząca się wzdłuż ściany kulka może być opisana tylko jedną liczbą: 70 cm od rogu pokoju. Jeżeli ta sama kulka zacznie toczyć się na ukos, trzeba podać jej odległości od obu ścian pokoju. W przypadku, gdyby ta sama kulka spadała z sufitu, potrzebne są aż trzy liczby, aby podać jej prawidłowe położenie w tej przestrzeni.
Istotne jest również miejsce położenia środka układu odniesienia, czyli punktu zerowego. Zazwyczaj wybieramy w tym celu obiekt nieruchomy, na przykład róg pokoju.
Ale układ odniesienia również może być ruchomy, na przykład związany z jadącym z naprzeciwka samochodem. Wtedy, względem niego, obiekt będzie poruszał się inaczej. Względem lecącego na niebie helikoptera - jeszcze inaczej. A względem samego siebie w ogóle nie będzie się przemieszczał - czy idąc, nawet dowolnie szybko, jesteśmy w stanie uciec od swojego ciała?
Tor, droga, przemieszczenie
Z pojęciem ruchu w fizyce jest związanych kilka ważnych określeń. Warto je znać, aby posługiwać się nimi prawidłowo.
Tor - tak nazywamy linię, którą tworzy w przestrzeni poruszające się ciało.
Droga - długość odcinka wyżej opisanej linii.
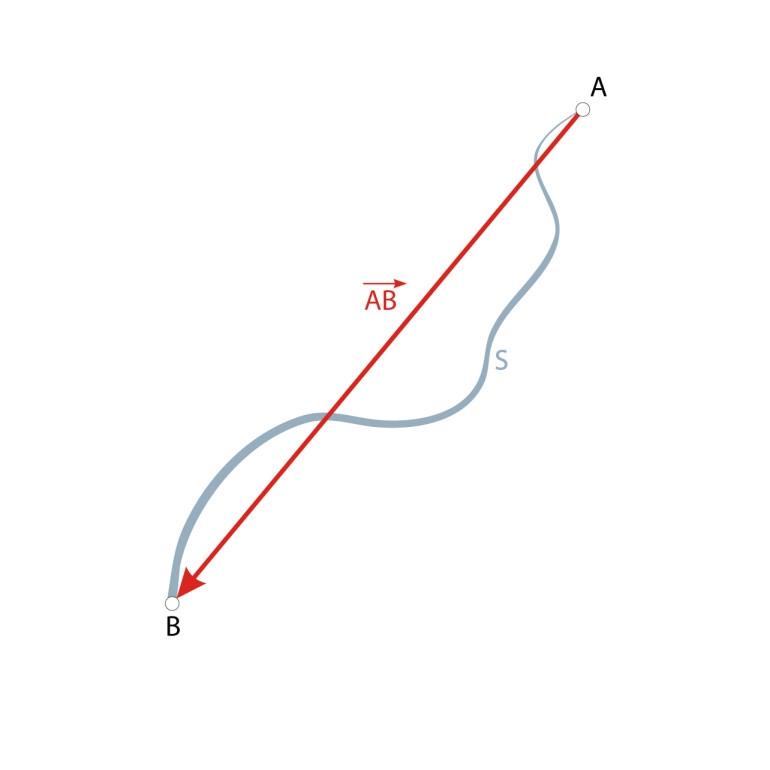
Przemieszczenie, zwane również wektorem przesunięcia - wektor zaczepiony w punkcie odpowiadającym początkowemu położeniu ciała, a którego koniec znajduje się w końcowym punkcie obserwacji.
Na powyższym rysunku, A to punkt początkowy, B to punkt końcowy. S to droga, zaś AB jest wektorem przemieszczenia.
Ruch i względność ruchu
Ruch - ciało fizyczne znajduje się w ruchu, jeżeli zmienia swoje położenie w układzie odniesienia w określonym czasie.
Względność ruchu - wspomniana już wcześniej dowolność wyboru układu odniesienia.
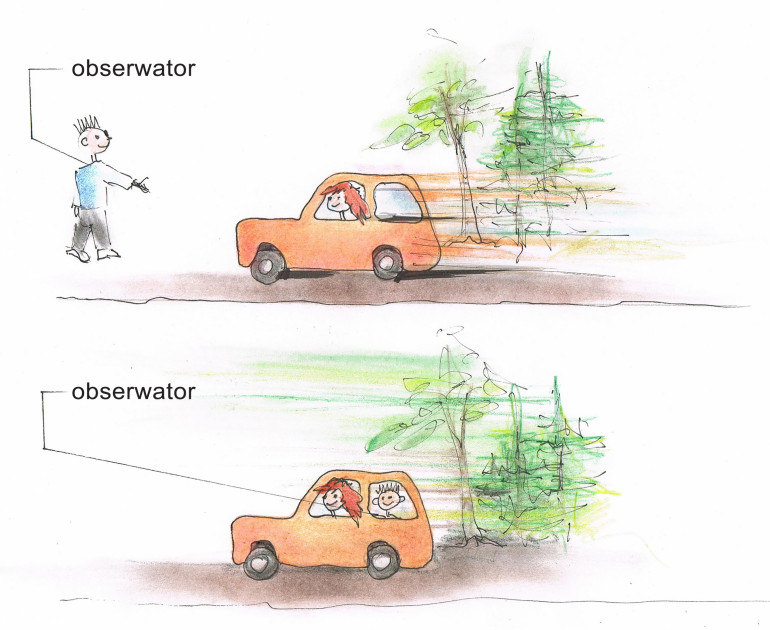
Obserwator stojący na drodze widzi zbliżający się do niego samochód. Jeżeli ten sam obserwator znajdzie się w środku samochodu, nie będzie się względem niego poruszał. Samochód stanie się dla niego nieruchomy, za to zacznie poruszać się całe otoczenie. Dokładniej, będzie przesuwać się do tyłu.
Czym jest prędkość?
To wielkość wektorowa - zawierająca informację również o kierunku i zwrocie. W ruchu jednostajnym prostoliniowym, czyli kiedy prędkość nie ulega zmianie i ruch odbywa się po linii prostej, ma wartość stałą. Można ją wtedy obliczyć z prostej zależności. Wystarczy podzielić wektor przemieszczenia przez czas trwania tego ruchu.
Tak samo obliczamy prędkość średnią, czyli kiedy jej wartość ulegała zmianie w trakcie ruchu, lecz interesuje nas jedynie efekt końcowy: z jaką prędkością ciało zmieniło swoje położenie, bez wnikania w szczegóły.
Szybkość
Na początku wspomniałem o zgubnych synonimach i to jest jeden z nich. Szybkość i prędkość dla fizyka to nie jest to samo. Prędkość jest wielkością wektorową, zaś szybkość to jedynie wartość liczbowa prędkości, długość tego wektora.
Zwłaszcza często interesuje nas szybkość średnia, na przykład w trakcie jazdy na wakacje. Wtedy żadnych wektorów nie stosujemy, jedynie dzielimy przyrost drogi przez przyrost czasu. Albo jeszcze prościej: drogę przez czas.
Jednostka
Według układu SI, jednostką zarówno prędkości, jak i szybkości, jest metr na sekundę [m/s]. Jednak życie wymusza na nas pewne uproszczenia, które nadal są zgodne z fizyką. Przykładem jest bardzo popularny w samochodach kilometr na godzinę [km/h] albo kilometr na sekundę [km/s] w przypadku samolotów ponaddźwiękowych. Z kolei, lądy dryfują z szybkością rzędu milimetrów na rok [mm/rok].
Przykład
Droga z siedziby AVT przy ulicy Leszczynowej w Warszawie do molo w Sopocie ma długość 342 km. Na jej przejechanie potrzeba 4 h. Jaka będzie wtedy średnia szybkość samochodu?
Dane:
s = 342 km
t = 4 h
Szukane:
v = ?
Obliczenia:
v = s / t
v = 342 km / 4 h
v = 85,5 km/h
Według powyższych obliczeń, średnia szybkość wyniesie 85,5km/h. W mieście, na obszarze zabudowanym, będzie niższa lub niekiedy wręcz zerowa (na przykład czekając na skrzyżowaniu), lecz na drodze ekspresowej będzie mogła być wyższa. Dlatego często interesuje nas wartość średnia.
Prędkość i szybkość chwilowa
Wartość średnia zazwyczaj odnosi się do jakiegoś długiego odcinka toru ruchu. Jednak w życiu mamy też do czynienia z wartością chwilową, czyli w danej chwili. Na przykład, szybkościomierz w samochodzie pokazuje właśnie szybkość chwilową.
Jeżeli auto zacznie hamować, jego wskazania również będą coraz mniejsze. Podczas przyspieszania, wskazówka unosi się, wskazując coraz to wyższe wartości szybkości. Większość drogowych fotoradarów mierzy właśnie szybkość chwilową, czyli zaobserwowaną na bardzo, bardzo krótkiej drodze. Jeżeli zostanie przekroczona ponad wartość przepisową, skończy się to mandatem.
Odcinkowy pomiar szybkości działa inaczej: mierzy czas przejazdu między dwiema bramkami, które są oddalone o zadany dystans. Jeżeli ten czas będzie zbyt krótki, oznacza to, że szybkość była zbyt wysoka i również trafi do nas stosowna kara.
Przyspieszenie
To ta część kinematyki, która pasjonatom samochodów kojarzy się najlepiej. I nic w tym dziwnego - przyspieszenie jest zmianą prędkości. Co ciekawe, może być dodatnie lub ujemne, o czym dalej.
Podstawowy wzór na przyspieszenie nie jest skomplikowany. To zmiana wektora prędkości podzielona przez czas, w którym się odbyła:
Jednak zazwyczaj posługujemy się tymi wzorami bez użycia wektorów, traktując przyspieszenie jako zwykłą wartość liczbową. Wystarczy wtedy pominąć strzałeczki nad oznaczeniami i nic więcej.
Jego jednostką jest [m/s2] - nie radzę wyobrażania sobie kwadratowych sekund, to tylko efekt matematycznych przekształceń. Analogicznie może powstać inna jednostka, na przykład [km/h2].
Objaśnienie
Przyspieszenie jest zmianą szybkości w czasie. Jeżeli a = 1 m/s2, to oznacza, że dane ciało stale zwiększa swoją szybkość: o 1 m/s co 1s. Obiekt poruszający się ze stałą szybkością rusza z miejsca natychmiast i nie zmienia swojej szybkości - wtedy przyspieszenie a = 0.
Jeżeli obiekt ruszył z miejsca z przyspieszeniem a = 1 m/s2 (początkowa szybkość v0 = 0), to jego szybkość rosła następująco:
- po upływie 1 s: v1 = 1 m/s,
- po upływie 2 s: v2 = 2 m/s,
- po upływie 3 s: v3 = 3 m/s
i tak dalej, czyli stale przyspieszał.
Inne wersje
Ruch jednostajnie przyspieszony, jaki został pokazany w powyższym przykładzie, to najprostsza wersja ruchu przyspieszonego. Może istnieć również ruch niejednostajnie przyspieszony, w którym mówimy o zmianie przyspieszenia w czasie. A nawet ta zmiana też może się zmieniać! Do takich opisów lepiej używać rachunku różniczkowego, by się w tym nie pogubić.
Ruch przyspieszony oznacza, że ciało przyspiesza, czyli jego szybkość rośnie. Ale może też istnieć ruch opóźniony (jednostajnie lub nie), kiedy szybkość maleje. Przyspieszenie takiego ciała jest wówczas ujemne: ujemny wzrost oznacza spadek.
Z ruchem przyspieszonym mamy zatem do czynienia podczas wzrostu szybkości, na przykład podczas ruszania samochodem. Z kolei ruch opóźniony występuje przy zmniejszaniu szybkości - przykładowo, podczas hamowania
Wzory
Z przyspieszeniem są związane użyteczne wzory, na przykład na szybkość w ruchu jednostajnie przyspieszonym, jeżeli nie występowała szybkość początkowa (v0 = 0)
Jeżeli szybkość nie była zerowa, lecz wynosiła v0, trzeba ją po prostu dodać do wyniku:
Droga przebyta przez ciało w ruchu jednostajnie przyspieszonym lub opóźnionym może być obliczona z takiej zależności. Jeżeli szybkość początkowa v0 = 0, trzeba ten składnik po prostu pominąć.
Podsumowanie
Kinematyka jest starą dziedziną fizyki, lecz nadal aktualną. Warto zaznajomić się z jej podstawami - chociażby po to, aby sprawnie posługiwać się określeniami, które mają dokładnie przypisane znaczenie. Zwłaszcza szybkość i prędkość często są mylone, co jest błędem.