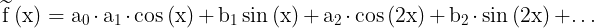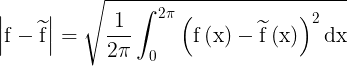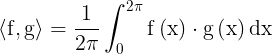Edukacja w EdW dla szkół i uczelni - wykład 37: Szeregi Fouriera

Jos Verstraten

Kursy

2 stycznia 2026

Jednym z najbardziej zaskakujących zjawisk w elektrotechnice jest fakt, że każdy sygnał okresowy można przedstawić jako sumę idealnych składowych sinusoidalnych i kosinusoidalnych. W niniejszym artykule podejmujemy próbę przystępnego wyjaśnienia tej złożonej teorii Fouriera, bez odwoływania się do aparatu matematycznego.

W artykule celowo zastosowano uproszczoną notację sygnałów sinusoidalnych i kosinusoidalnych, odbiegającą od ścisłego zapisu matematycznego funkcji czasu. Zabieg ten ma charakter dydaktyczny i wynika z chęci przybliżenia idei szeregów Fouriera w sposób intuicyjny, bez odwoływania się do aparatu matematycznego. W prezentowanej konwencji zapisy typu sin(f) i cos(f) należy rozumieć jako skrótowe oznaczenia składowych o określonej częstotliwości, a nie jako formalne wzory matematyczne.

Poprzednia część

Spis treści

Następna część Toc right icon

Rozwiń cały spis treści Zwiń spis treści

Co odkrył Fourier?

Jean-Baptiste Joseph Fourier był francuskim matematykiem i fizykiem, urodzonym w 1768 roku. Największą sławę przyniosły mu analiza Fouriera oraz transformata Fouriera, które do dziś noszą jego nazwisko.

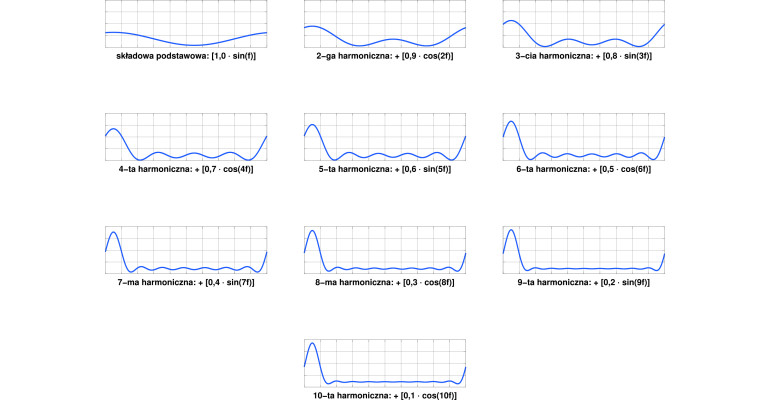
Gdy słuchamy dźwięku o określonej częstotliwości – na przykład tonu powstającego podczas drgań struny skrzypiec – łatwo zauważyć, że ten sam dźwięk może brzmieć zupełnie inaczej, jeśli zostanie zagrany na innym instrumencie. Skąd bierze się ta różnica? Okazuje się, że dany ton nie jest tworzony wyłącznie przez drgania struny o częstotliwości podstawowej. O jego barwie decyduje przede wszystkim obecność tak zwanych alikwotów, czyli drgań o częstotliwościach będących całkowitymi wielokrotnościami częstotliwości tonu podstawowego. Drgania te nazywa się harmonicznymi.

O tym, jak odbieramy brzmienie danego instrumentu, decydują wzajemne proporcje amplitud składowej podstawowej i poszczególnych harmonicznych. Tę charakterystyczną kombinację można obrazowo porównać do swoistego „profilu DNA” instrumentu.

Fourier wykazał – w sposób matematycznie bardzo złożony – że każdy sygnał okresowy można przedstawić jako sumę sygnałów sinusoidalnych lub kosinusoidalnych o częstotliwości podstawowej oraz wielu harmonicznych. Podobnie jak w przypadku instrumentów muzycznych taka struktura decyduje o barwie dźwięku, tak samo określa ona kształt przebiegu sygnału okresowego. Zbiór tych wzajemnych proporcji między składową podstawową a harmonicznymi nazywamy szeregiem Fouriera danego sygnału.

Fourier to bardzo dużo matematyki

Jeśli – nie mając przygotowania matematycznego – próbowaliście kiedyś znaleźć w Internecie przystępne wyjaśnienie zagadnień związanych z Fourierem, analizą Fouriera lub szeregami Fouriera, to niemal na pewno trafiliście na strony wyglądające mniej więcej tak:

Teoria

Pytanie brzmi, czy istnieje systematyczny sposób przybliżania funkcji okresowej f – przyjmujemy tu okres 2π – za pomocą szeregu trygonometrycznego, to znaczy szeregu postaci:

Współczynniki tego szeregu należy dobrać w taki sposób, aby odległość między funkcją f a szeregiem była możliwie najmniejsza, przy czym odległość ta jest zdefiniowana za pomocą formuły:

Rozważania można uprościć, zauważając, że norma ta jest indukowana przez iloczyn wewnętrzny:

Względem tak zdefiniowanego iloczynu wewnętrznego funkcje sinus i kosinus – przy czym funkcję stałą traktuje się jako cos(0x) – tworzą układ ortogonalny. Dzięki temu poszukiwany szereg otrzymuje się jako rzut ortogonalny funkcji f na przestrzeń rozpiętą przez poszczególne funkcje sinus i kosinus.

Tak właśnie na Wikipedii omawiane jest pojęcie „szeregu Fouriera”. Nie jest to lektura szczególnie zachęcająca – ani do czytania, ani tym bardziej do zrozumienia. Dlatego podejmujemy próbę wyjaśnienia tego ważnego pojęcia z zakresu elektroniki w sposób pozbawiony matematycznych formalizmów. Fakt, że Czytelnik lub Czytelniczka z solidnym przygotowaniem matematycznym mogą miejscami łapać się za głowę, przyjmujemy z góry jako nieunikniony koszt takiego podejścia.