Wokół Arduino: napisy i inne zakrętasy cz.1 - liczby dwójkowe i tekst oraz kodowanie ASCII

Piotr Górecki

Kursy

15 października 2018

453

Zajmiemy się napisami – łańcuchami tekstowymi. Z jednej strony wiemy, że w komputerze wszystkie dane to zera i jedynki. A przy komunikacji komputer–człowiek (mikroprocesor–człowiek) na ekranie trzeba wyświetlić napisy i liczby w sposób zrozumiały dla człowieka. Na pewno nie w postaci ciągów zer i jedynek. Z kolei w drugim kierunku trzeba wprowadzić do komputera/ procesora teksty i liczby – zapewne właśnie w postaci zer i jedynek, bo jakże mogłoby być inaczej. To bardzo obszerne zagadnienie można podzielić na dwie, a raczej trzy odrębne części.

Poprzednia część

Spis treści

Następna część

1. Wokół Arduino: napisy i inne zakrętasy cz.1 - liczby dwójkowe i tekst oraz kodowanie ASCII 2. Wokół Arduino: napisy i inne zakrętasy cz.2 - wyświetlacz HD44780, liczby i cyfry, metody .print() i .write() 3. Wokół Arduino: napisy i inne zakrętasy cz.3 - co to jest Unicode? 4. Wokół Arduino: napisy i inne zakrętasy cz.4 - Jak numer znaku w unikod jest reprezentowany w UTF-8?

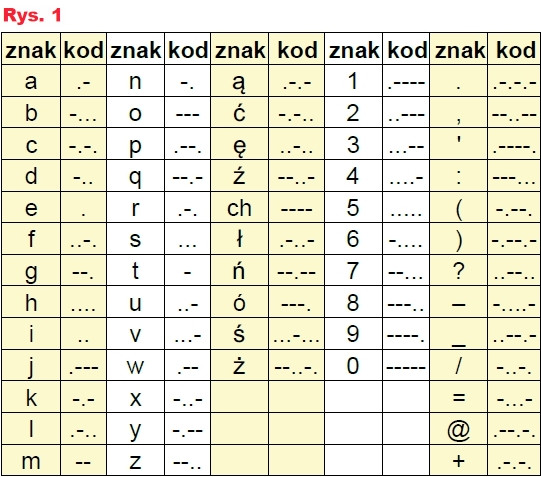
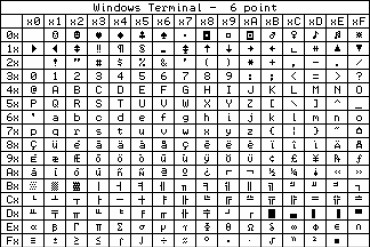
Jedna sprawa to teksty, mówiąc w uproszczeniu: napisy składające się z liter (ale też innych znaków). Druga sprawa to liczby. I tu mamy dwie dodatkowe odrębne kwestie. Jedna to sprawa liczb „mniejszych, większych, ułamkowych” oraz sposób ich reprezentacji w komputerze za pomocą zer i jedynek. W grę wchodzą tu typy zmiennych (m.in. byte, char, int, long, float, double) i tym bardzo ważnym zagadnieniem zajmiemy się w oddzielnych artykułach. A teraz przyjmujemy tylko, że w komputerze/procesorze mamy rozmaite liczby, a wszystkie w sumie są mniejszymi i większymi zbiorami zer i jedynek.

W tym artykule zajmiemy się drugim aspektem związanym z liczbami. Otóż teraz nie interesują nas szczegóły, jak liczby są reprezentowane/kodowane w procesorze i jego pamięci, tylko interesuje nas dwustronna komunikacja, przesyłanie, przekazywanie na drodze procesor–człowiek (człowiek–procesor) zarówno wartości liczbowych, jak też napisów – tekstów.