Podsumowanie: stosunek zwojów
Zależność między pierwotnym oraz wtórnym napięciami i prądami dla idealnej transformacji jest określona przez stosunek ilości zwojów. Dla pierwotnego napięcia i prądu (up, ip) przyłożonego do uzwojenia ze zwojami NP i uzwojenia wtórnego ze zwojami NS, napięcie i prąd wtórny będą wynosić:
Idealny transformator ma sprawność 100%, więc moc wejściowa będzie równa mocy wyjściowej, choć rzeczywiste transformatory nie mają oczywiście takiej sprawności.
Transformatory składają się z zestawu cewek, a cewki same w sobie są induktorami. Indukcyjność cewki (L) jest powiązana z kwadratem liczby zwojów (N2), ale konkretna zależność zależy od ich rodzaju, budowy i wymiarów. Ogólnie możemy zapisać L=kN2, więc N=√(L/k), gdzie k jest stałą. W przypadku idealnego transformatora możemy założyć, że k jest takie samo dla uzwojenia pierwotnego i wtórnego, więc:
Stosunek zwojów jest równy pierwiastkowi kwadratowemu stosunku indukcyjności uzwojeń (rozważanych jako pojedyncze cewki indukcyjne). Ten stosunek indukcyjności jest ważny przy konfigurowaniu transformatorów w symulacjach SPICE.
Impedancja odbita i model transformatora
Jak wspomniano w pierwszym artykule, transformatory przenoszą impedancje z jednego uzwojenia do drugiego. Na przykład, jeśli podłączymy rezystor obciążenia (RL) do obwodu wtórnego, wówczas obwód sterujący uzwojeniem pierwotnym wykryje skuteczną rezystancję (R’L). Widziany od strony pierwotnej opór jest określony przez kwadrat stosunku zwojów, więc w tym przypadku:
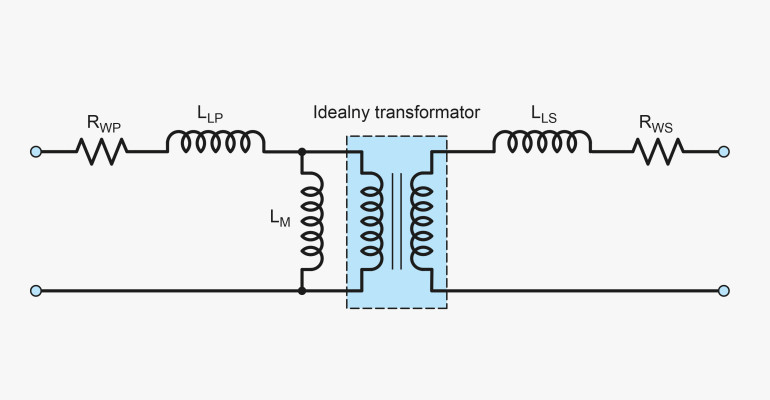
W przypadku idealnego transformatora w tym przykładzie rezystancja „widziana” na uzwojeniu pierwotnym wynosi po prostu R’L, ale rzeczywiste transformatory mają pewną rezystancję uzwojenia (zwaną także „rezystancją dla prądu stałego”, aby odróżnić ją od zjawisk takich jak indukcyjność rozproszenia). Rezystancja uzwojenia wtórnego dla prądu stałego (RWS) pojawi się szeregowo z RL i będzie widoczna w uzwojeniu pierwotnym w ten sam sposób. Rezystancja uzwojenia pierwotnego dla prądu stałego (RWP) będzie połączona szeregowo z całkowitą rezystancją przeniesioną. Jeśli uzwojenie wtórne jest zwarte (więc R’L=0), wówczas uzwojenie pierwotne będzie postrzegane jako odbita rezystancja uzwojenia wtórnego i pierwotnego. Na przykład w przypadku transformatora 1:1 z obydwoma uzwojeniami o rezystancji prądu stałego 100 Ω, uzwojenie pierwotne będzie wyglądało jak rezystor 200 Ω ze zwartym uzwojeniem wtórnym. Pomimo konstrukcji z wykorzystaniem cewek, jeśli jedyną niedoskonałością jest rezystancja prądu stałego, transformator z rezystorem obciążającym na uzwojeniu wtórnym będzie zachowywał się jak rezystor, ale w rzeczywistości transformatory mają więcej cech niż tylko rezystancja uzwojenia prądu stałego.
Jeśli uzwojenie wtórne jest obwodem otwartym, wówczas uzwojenie pierwotne prawdziwego transformatora można zamodelować jako cewkę indukcyjną (LM) wpiętą równolegle do (idealnego) uzwojenia pierwotnego i szeregowo z rezystancją uzwojenia pierwotnego, więc nie zachowuje się jak obwód otwarty po stronie pierwotnej. Indukcyjność ta nazywana jest „indukcyjnością magnesowania”. W sytuacjach, gdzie obwód nie jest otwarty, impedancja ta może być wystarczająco duża, aby mieć pewien niewielki wpływ na całkowitą impedancję obserwowaną w uzwojeniu pierwotnym (jeśli jest równoległa do znacznie mniejszego R’L). Wspominając o indukcyjności magnesowania, warto zauważyć, że kolejną nieidealną indukcyjnością stosowaną do modelowania rzeczywistych transformatorów jest indukcyjność rozproszenia, która jest połączona szeregowo z obydwoma uzwojeniami (LLS i LLP) – jest to spowodowane przez nieidealne sprzężenie magnetyczne pomiędzy dwoma uzwojeniami.