W poprzednim artykule badaliśmy widma sygnałów w kontekście zniekształceń. Widmo jest to rozkład natężenia sygnału w funkcji częstotliwości, ukazujący jakie częstotliwości składowe występują w sygnale. Każdy przebieg okresowy można utworzyć poprzez zsumowanie pewnej ilości fal sinusoidalnych o różnych częstotliwościach i amplitudach. Ta suma znana jest jako szereg Fouriera. Wykres widma sygnału okresowego jest zbiorem prążków położonych przy określonych częstotliwościach.
Widmo na wyjściu układu liniowego nie będzie zawierało częstotliwości, które nie występowały na wejściu – chociaż względne amplitudy oryginalnych częstotliwości mogą ulec zmianie. Jeśli z powodu nieliniowości układu występują zniekształcenia sygnału, na wyjściu pojawią się częstotliwości, których na wejściu nie było. W przypadku sinusoidalnego sygnału wejściowego, dodatkowe częstotliwości na wyjściu będą wielokrotnościami częstotliwości wejściowej, czyli harmonicznymi sygnału wejściowego. Jest to podstawa ilościowego określenia zniekształceń poprzez współczynnik THD. Wykreślenie widma sygnału i obliczenie THD jest możliwe w symulatorze LTspice. Użycie LTspice zapewnia wszechstronny wgląd w zagadnienie zniekształceń. Posługiwanie się symulatorem wymaga jednak pewnej uwagi i ostrożności, co było w zeszłym odcinku kluczowym elementem dyskusji.
Zniekształcenia są na ogół niepożądane. Mają one jednak swoje zastosowania, między innymi w efektach dźwiękowych wykorzystywanych przez muzyków. Chyba najbardziej znanym przykładem są podłogowe efekty zniekształcające używane przez gitarzystów elektrycznych. Niniejsza seria artykułów została w istocie zainspirowana układami do efektów muzycznych autorstwa Johna Clarke’a, zamieszczanymi w „Practical Electronics” w ciągu ostatnich dwóch lat. W tym miesiącu przyjrzymy się układom, które można wykorzystać do zamierzonego wytwarzania zniekształceń.
Obcinanie
Większość zniekształceń w zastosowaniach muzycznych uzyskuje się z pomocą układów, które powodują obcinanie sygnału. Amplituda przebiegu zostaje tak ograniczona, że jego szczyty ulegają spłaszczeniu. Efekt ten bywa również nazywany „nasyceniem„. Zanim jednak przejdziemy do omówienia układów, które można wykorzystać do uzyskania takiego efektu, podsumujmy, co rozumiemy przez obcinanie, i przyjrzyjmy się kilku zasadniczym jego odmianom („twarde”/„miękkie” i symetryczne/asymetryczne).
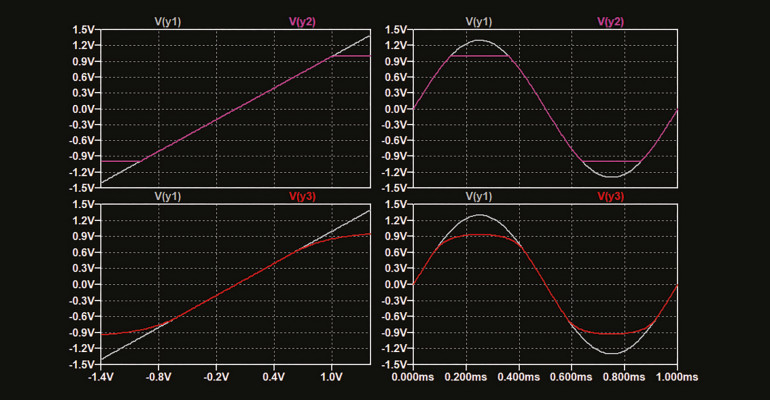
Jeśli dla idealnego wzmacniacza wykreślimy funkcję przenoszenia (napięcie wyjściowe w funkcji napięcia wejściowego), będzie ona dla wszystkich możliwych napięć idealną linią prostą (szara linia V(y1) na wykresach po lewej stronie rysunku).
Wzmacniacze rzeczywiste cechuje jednak określona maksymalna amplituda wyjściowa, co powoduje, że ich funkcje przenoszenia są podobne do tych pokazanych przez kolorowe krzywe V(y2) i V(y3) po lewej stronie rysunku. Obie krzywe różnią się między sobą ostrością przejścia od obszaru liniowego (dla małych amplitud) do obszaru pełnego ograniczania (dla dużych amplitud). Przechodzenie stosunkowo szybkie (jak krzywa y2) nazywane jest „obcinaniem twardym” (ang. „hard clipping”; przypis redaktora). Do przechodzenia bardziej stopniowego (jak krzywa y3) odnosi się określenie „obcinanie miękkie” (ang. „soft clipping”; przypis redaktora). Wykresy na rysunku powyżej uzyskano w oparciu o matematycznie zdefiniowaną funkcję przenoszenia, omówioną w pierwszym artykule tego cyklu. Szare krzywe po prawej stronie rysunku ukazują niezniekształconą falę sinusoidalną na wyjściu.
W przypadku konkretnego wzmacniacza – lub innego układu, który wprowadza obcinanie – stopień zniekształceń zależy od amplitudy sygnału wejściowego. Ilustruje to rysunek poniżej, na którym widać przebieg wyjściowy układu o tej samej funkcji przenoszenia, co na rysunku powyżej, ale przy ponad dwukrotnie większej wartości szczytowej na wejściu. Wraz ze wzrostem amplitudy sinusoidalnego sygnału wejściowego, przebieg na wyjściu układu przesterowującego ma tendencję do stawania się falą prostokątną. Łagodniejsza funkcja przesterowania sprawia, że narożniki fali prostokątnej są zaokrąglone. Taki sam efekt da filtrowanie sygnału zniekształconego w filtrze dolnoprzepustowym.
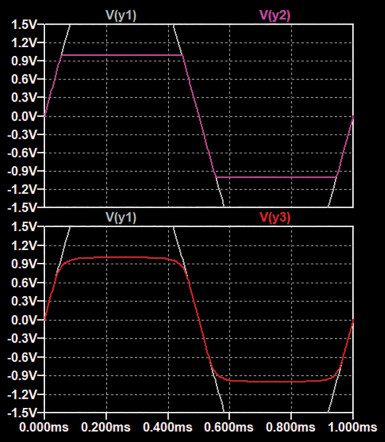
Funkcja przenoszenia układu zniekształcającego nie musi być symetryczna. Jeśli będzie ona asymetryczna, wystąpi niesymetryczne zniekształcenie. Ten sam efekt da wysterowanie układu o symetrycznej funkcji przenoszenia sygnałem z nałożoną składową stałą.