Wymagane informacje podstawowe
Czy terminy takie jak charakterystyka amplitudowa, częstotliwość odcięcia, dB/oktawę, filtr drugiego rzędu, wykres Bode’a i filtr Butterwortha nic dla Ciebie nie znaczą? W takim razie zdecydowanie zalecamy zapoznać się z dzisiejszym materiałem. W artykule przedstawiono ogólne koncepcje filtrów analogowych.
Filtr pasmowo-przepustowy
Wprowadzenie. Filtry pasmowo-przepustowe można podzielić na dwie główne grupy:
- filtry wąskopasmowe,
- filtry szerokopasmowe.
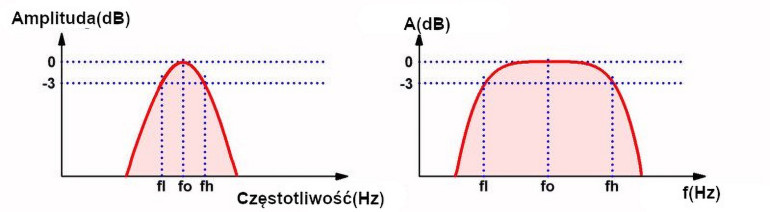
Różnica między tymi dwoma filtrami została przedstawiona na poniższym rysunku. Po lewej stronie narysowano filtr wąskopasmowy, a po prawej szerokopasmowy. Trudno jest określić, gdzie kończy się definicja filtra wąskopasmowego, a zaczyna ta dotycząca szerokopasmowego. W większości przypadków filtr szerokopasmowy ma „płaski wierzchołek” w swojej charakterystyce amplitudowej.
Szerokość pasma B. Istnieje pewien zakres częstotliwości, dla którego wzmocnienie filtra jest maksymalne. Wzmocnienie to jest zwykle ustawione na 0 dB. Główną cechą filtra pasmowo-przepustowego jest jego szerokość pasma B. Jest to zakres częstotliwości, dla którego tłumienie filtra jest mniejsze niż –3 dB, mierzone względem częstotliwości środkowej filtra f0. Na powyższych wykresach szerokość pasma jest zatem zdefiniowana przez obszar między częstotliwościami fl i fh.
Szerokość pasma zmniejsza się, gdy filtr staje się węższy.
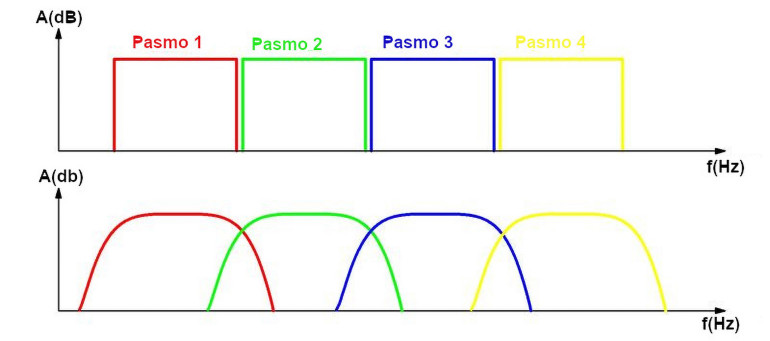
Stromość filtra pasmowo-przepustowego. Inną ważną cechą filtra pasmowo-przepustowego jest jego stromość. Jest to nachylenie, przy którym sygnały o częstotliwościach spoza szerokości pasma są tłumione. Stopień pożądanej stromości zależy od zastosowania filtra pasmowo-przepustowego. Jeśli używasz wielu identycznych filtrów pasmowo-przepustowych do stworzenia analizatora widma dźwięku na wielu słupkach LED, wówczas stromość filtrów powinna być jak największa. Wyjaśniają to wykresy na poniższym rysunku. Na górnym wykresie przedstawiono idealną odpowiedź czterech filtrów pasmowoprzepustowych. Filtry mają nieskończenie dużą stromość; cały zakres częstotliwości jest starannie podzielony na cztery podobszary bez nakładania się czterech filtrów pasmowo-przepustowych.
Na dolnym wykresie przedstawiono charakterystyki amplitudowe czterech filtrów pasmowo-przepustowych o niskiej stromości. Charakterystyki te w dużym stopniu nakładają się na siebie, więc niektóre sygnały o częstotliwościach wypadających między teoretycznymi pasmami będą wyświetlane na słupkach LED błędnie.
Współcześnie w analizatorach widma nie stosuje się już analogowych filtrów pasmowo-przepustowych, lecz używa się cyfrowego przetwarzania sygnałów z szybką transformatą Fouriera. Również hobbyści sięgają po takie rozwiązania, i są dostępne gotowe projekty oparte o płytki Arduino, ESP8266/ESP32 czy STM32. Przyp. tłum.
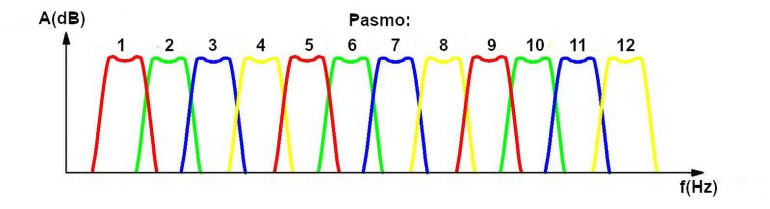
Strome filtry nie zawsze są pożądane. Jeśli jednak używasz filtrów pasmowych do dzielenia sygnału audio na kilka pasm, które kontrolują kanały organów świetlnych, wówczas bardzo strome filtry są niepotrzebne, a nawet niepożądane. Wyjaśnia to wykres na poniższym rysunku. W takich zastosowaniach należy zaprojektować filtry pasmowe tak, aby zachodziły na siebie. Zapewnia to pożądaną grę kolorów w organach świetlnych w funkcji częstotliwości sygnału muzycznego.
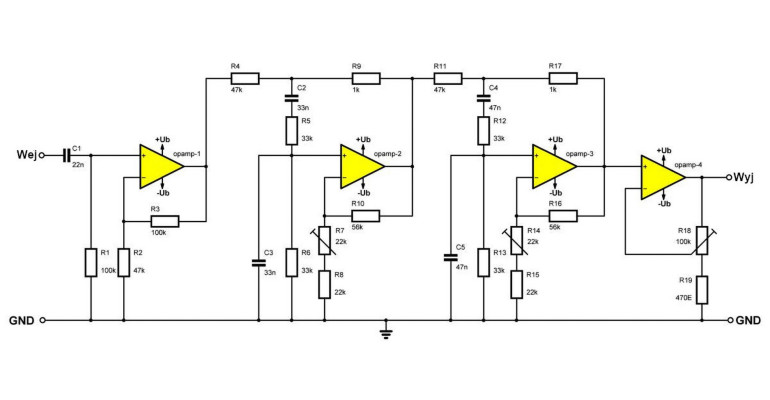
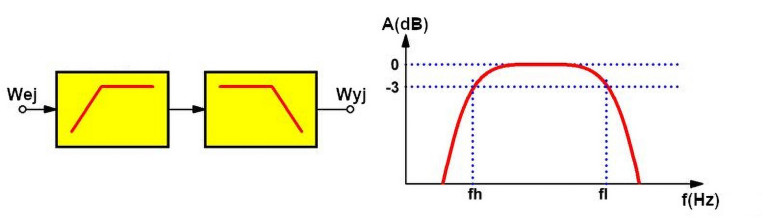
Szerokopasmowy filtr pasmowo-przepustowy. Filtr szerokopasmowy powstaje, jak pokazano na poniższym rysunku, przez połączenie w odpowiedniej kolejności filtra dolnoprzepustowego i górnoprzepustowego. Jak wynika z charakterystyki amplitudowej, istnieją teraz dwie częstotliwości odcięcia fl i fh, które określają szerokość pasma B obwodu. Częstotliwość fh jest częstotliwością odcięcia filtra górnoprzepustowego, fl jest częstotliwością odcięcia filtra dolnoprzepustowego. Aby obwód działał jako filtr pasmowo-przepustowy tylko wtedy, gdy fh jest mniejsza niż fl. Należy oczywiście dokładnie dopasować charakterystyki obu podfiltrów. Oznacza to, że należy użyć tej samej topologii filtra dla obu filtrów. Wybór topologii zależy od stromości, jaką chcemy nadać filtrowi (i innych pożądanych parametrów – przyp. tłum.). W przypadku bardzo stromych filtrów należy oczywiście użyć topologii Chebysheva.