Chirurgia obwodowa. Rozwiązywanie obwodu: iteracyjne proste obciążenia i symulacja

Ian Bell

Kursy

Podstawy elektroniki

31 stycznia 2024

138

Prosta obciążenia, to graficzny sposób rozwiązywania problemu zachowania się obwodu bez konieczności przeprowadzania jego szczegółowej analizy matematycznej. W tym artykule przyjrzymy się prostym obciążenia w kontekście różnych sposobów rozwiązywania obwodów nieliniowych – w szczególności obwodu dioda-rezystor pokazanego na rysunku.

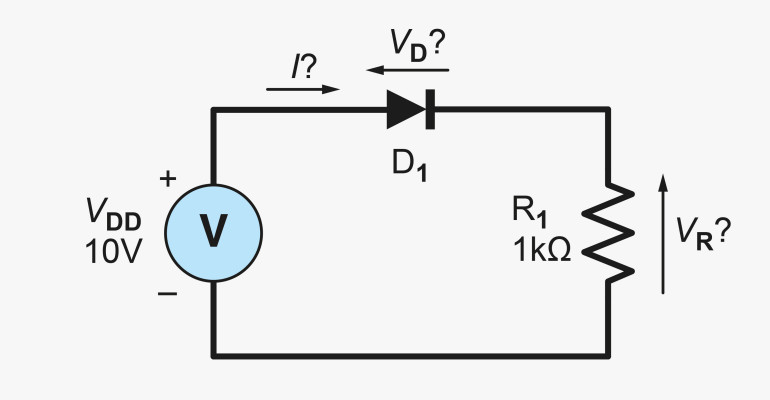
Jest to obwód prosty – dioda spolaryzowana w kierunku przewodzenia, czyli dioda, przez którą prąd płynie w kierunku wskazanym przez kształt strzałki symbolu diody. Zakładając, że znamy podstawową teorię obwodów, zależności napięcie-prąd diody i rezystora oraz wartości parametrów charakterystycznych diody, możemy założyć, że łatwo będzie znaleźć równanie prądu w obwodzie przedstawionym na rysunku otwierającym. Gdyby zamiast diody i rezystora były dwa rezystory, byłoby to łatwe dzięki podstawowej teorii obwodów; okazuje się jednak, że „rozwiązanie” obwodu diodowego nie jest takie proste.

Zanim przejdziemy do szczegółów obwodu z diodą, przejrzymy potrzebną nam teorię obwodów i rozwiążemy obwód z dwoma rezystorami jako punkt odniesienia. Dwie z kluczowych zasad analizy obwodów znane są jako prawa Kirchhoffa (pochodzące z 1854 r.). Jedno z praw stanowi, że „suma prądów wpływających do węzła w obwodzie wynosi zero (lub całkowity prąd wejściowy = całkowity prąd wyjściowy)”. Oznacza to również, że prąd płynący przez zestaw elementów połączonych szeregowo jest taki sam w każdym elemencie (prądy diody i rezystora są równe w obwodzie na powyżej). Drugie prawo stanowi, że „suma napięć wokół dowolnej pętli w obwodzie wynosi zero”.

Prawa obwodowe i modele elementów

Prawa Kirchhoffa dotyczą zarówno napięcia, jak i prądu. Aby w pełni przeanalizować obwód, musimy znać zależności między prądami i napięciami w obwodzie. Zależności te opisują równania charakterystyczne poszczególnych składników. W naszym przykładzie charakterystyczne równanie rezystora to U=IR, co wielu czytelników rozpozna jako prawo Ohma. Na przykład dla rysunku powyżej możemy napisać: UR=IR1.

Prawo Ohma, a co za tym idzie także charakterystyczne równanie rezystora, zostało po raz pierwszy uzyskane eksperymentalnie przez Georga Ohma w latach dwudziestych XIX wieku. Można je również wyprowadzić z podstawowej fizyki przewodników, chociaż historycznie stało się to znacznie później. W przypadku prawdziwego rezystora prawo Ohma jest tylko przybliżeniem, rezystancja może w rzeczywistości zmieniać się wraz z przyłożonym napięciem i prawdopodobnie będzie się zmieniać wraz z temperaturą, w tym również spowodowaną samonagrzewaniem rezystora. Ponadto rezystory generują szum elektryczny, a prawo Ohma dotyczy tylko średniego prądu. Matematyczny sposób, w jaki wybieramy reprezentację komponentu, nazywany jest „modelem” tego komponentu.

W większości przypadków w przypadku elementów rezystancyjnych używanych w obwodach możemy po prostu użyć zależności U=IR w analizie obwodów. Jeśli zdecydujemy się uwzględnić w naszych obliczeniach inne czynniki (i zrobimy to poprawnie), otrzymamy dokładniejsze wyniki kosztem większej trudności i złożoności obliczeniowej. W przypadku obliczeń ręcznych zbyt duża złożoność może sprawić, że proces będzie podatny na błędy lub nawet trudny do wykonania, a w przypadku analizy komputerowej (symulacja obwodów) czasy wykonywania wydłużają się dla bardziej złożonych modeli. Jak zawsze w inżynierii, istnieją kompromisy – w tym przypadku pomiędzy dokładnością a złożonością.

W równaniu charakterystycznym rezystora U=IR–R (rezystancja) jest ogólnie określane jako „parametr” (lub parametr modelu). Wszystkie równania charakterystyki składowej będą miały jeden lub więcej parametrów. Możemy analizować obwód algebraicznie, używając symboli parametrów (np. R1, R2… dla rezystorów), ale jeśli potrzebujemy znać rzeczywiste napięcia i prądy, musimy podać określone wartości parametrów dla każdego elementu.