Zaloguj się
Wszystkie
18 lutego 2019
1973
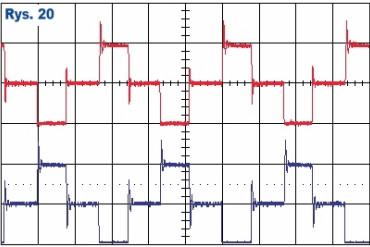
Jeden z Czytelników od razu zareagował na to, co było przedstawione w styczniowej rubryce Poczta:
(...) Wielkie moje zdziwienie wzbudziło zalecenie, aby transformatorów nie załączać przy przejściu napięcia przez zero, a przy maksimum sinusoidy. Dla prądu zmiennego obowiązuje zależność I=U/Z, a więc przy przejściu przez zero nie dzieje się nic, nie ma napięcia, nie ma prądu. Skutki załączania w dowolnym miejscu sinusoidy znają zapewne wszyscy budujący układy tyrystorowe z regulacją fazową, generujące bardzo kłopotliwe do usunięcia zakłócenia impulsowe. Tam, gdzie to jest możliwe, stosuje się sterowanie grupowe i w tym celu opracowano układy (optotriaki) z załączaniem w zerze np. MOC3042 itp.
Przekonanie, że układy elektroniczne najlepiej włączać w momencie przejścia napięcia sieci przez zero, rzeczywiście ma mocne podstawy, zarówno teoretyczne, jak i praktyczne. Zdrowa logika podpowiada, że gdy nie ma napięcia, to nie ma i prądu, a dołączenie obciążenia w chwili, gdy napięcie jest...
Facebook
Twitter
Linkedin
Kup teraz
