Zaloguj się
Wszystkie
3 czerwca 2024
88
Jaki jest potencjał elektryczny?
Mechaniczny odpowiednik
Aby zrozumieć pojęcie potencjału elektrycznego, należy powrócić do mechaniki klasycznej. Jeśli podniesiesz kulę z ziemi i uniesiesz ją na wysokość jednego metra, musisz wykonać pracę lub zużyć energię. Energia ta jest niejako zmagazynowana w kuli, ponieważ jeśli ją puścimy, spadnie, co oczywiście również wymaga energii. Energia, która jest potencjalnie obecna w kuli (lub jakimkolwiek innym obiekcie) nazywana jest energią potencjalną. Obiekt jest w stanie dostarczyć energię, gdy zostaną stworzone ku temu odpowiednie warunki.
Elektryczna energia potencjalna
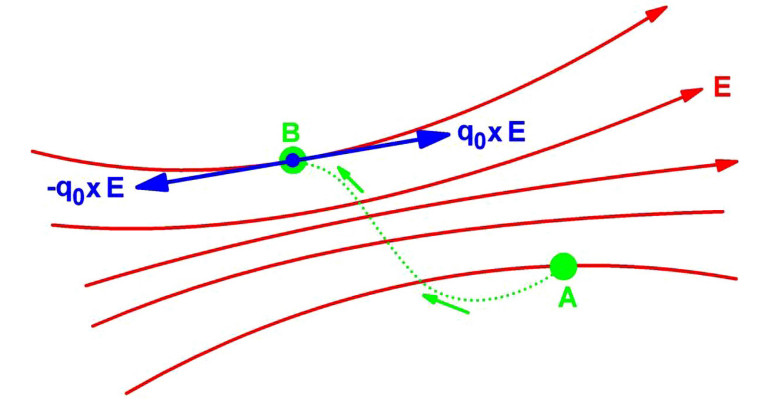
Ze względu na fizyczne znaczenie pojęcia energii poszukiwano możliwości wprowadzenia tego pojęcia do teorii elektryczności. Rozumowanie to wyjaśniono na poniższym rysunku. Załóżmy, że gdzieś w przestrzeni znajduje się pole elektryczne, które można oczywiście zdefiniować za pomocą natężenia pola elektrycznego E. Załóżmy teraz, że ładunek elektryczny q0 jest umieszczony w tym polu w punkcie A. Ładunek ten doświadczy siły Coulomba, która jest wyrażona wzorem:
F=q0·E
Aby przemieścić ładunek z punktu A do punktu B, do ładunku należy przyłożyć przeciwną siłę –F. Zgodnie z ogólnymi prawami mechaniki, praca do tego wymagana może być wyrażona tak:
W=–F·s
Gdzie s jest funkcją wektorową opisującą odległość przebytą przez ładunek.
W mechanice klasycznej, jeśli na spadającym ciele wykonamy pewną pracę wbrew sile grawitacji oddziałującej na to ciało, jego energia potencjalna wzrośnie o wartość wykonanej pracy W. Analogicznie jeśli na ładunku q0 wykonana zostanie określona praca w kierunku przeciwnym, niż oddziałuje na ten ładunek pole elektryczne, ten ładunek również zyska pewną energię potencjalną równą wykonanej pracy W. Ten wzrost energii potencjalnej ładunku nazywany jest elektrycznym potencjałem ładunku. Ta elektryczna energia potencjalna jest reprezentowana przez symbol U, a różnica energii między stanem w punkcie B i w punkcie A przez ΔU.
Co oznacza grecka litera Δ (delta)?
Δ to grecka litera wymawiana jako delta. W matematyce i fizyce Δ jest zawsze używane do wyrażania niewielkich różnic w wartości jednej i tej samej wielkości.
Facebook
Twitter
Linkedin
Kup teraz
