Zaloguj się
Wszystkie
4 lipca 2025
46
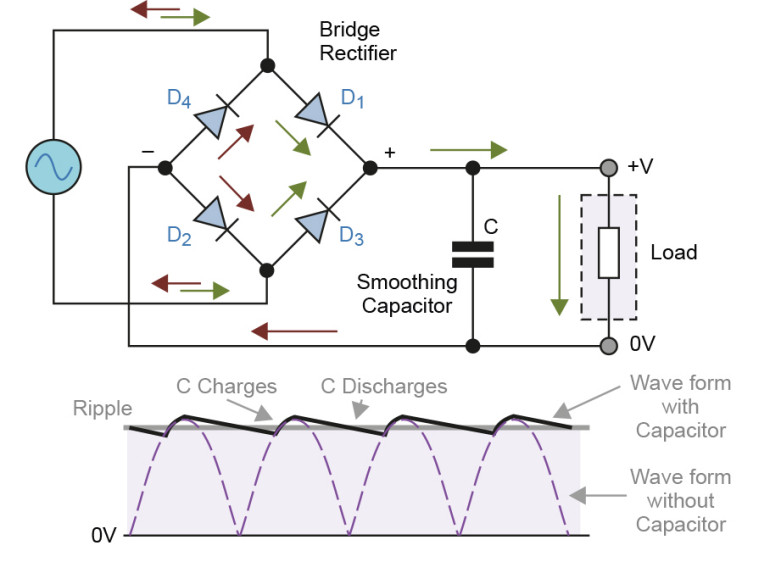
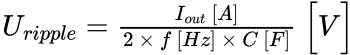Całkowicie typowa sytuacja: prostownik dwupołówkowy prostuje napięcie przemienne z transformatora, za prostownikiem znajduje się kondensator obciążony rezystancją imitującą zasilany układ. Schemat takiego tworu oraz przybliżony przebieg napięcia na zaciskach tegoż kondensatora pokazano na rysunku 1.
Najczęściej ten przykład przytacza się w nawiązaniu do prostowania napięcia sieciowego o częstotliwości 50 Hz (tudzież 60 Hz), lecz w przypadku przetwornic impulsowych te przebiegi również są podobne. Nie jest zagadką także działanie takiego filtra: kondensator zostaje doładowany impulsem prądu dostarczanym przez diody w trakcie dochodzenia napięcia do wartości maksymalnej, po czym się rozładowuje przez pozostałą część (czyli więcej niż połowę, bo napięcie na kondensatorze nie spada do zera) okresu napięcia wejściowego. Im większy jest prąd pobierany z kondensatora filtrującego, tym silniej ulegnie on rozładowaniu przed następnym ładowaniem. Warto również zauważyć, że krzywa narastania napięcia na kondensatorze w trakcie jego ładowania odtwarza dokładnie taki sam kształt, jak przebieg napięcia podanego na prostownik, z różnicą w postaci spadku napięcia na diodach prostowniczych.
Teraz pytanie: co zrobić, żeby składowa zmienna napięcia na kondensatorze miała możliwie małą amplitudę? O ile ładowanie zawsze przebiega dokładnie tak samo, o tyle wpływ mamy na część dotyczącą rozładowania. Im większa pojemność i/lub mniejszy prąd pobierany z prostownika, tym spadek napięcia wywołany rozładowaniem będzie niższy, o czym świadczy poniższy (uproszczony) wzór na wartość międzyszczytową napięcia tętnień w przypadku małej ich wartości:
gdzie: Iout to prąd pobierany z kondensatora filtrującego, f to częstotliwość napięcia przemiennego wchodzącego na prostownik, zaś C to oczywiście pojemność kondensatora filtru.
Wzór ten jest bardzo rozpowszechniony w internecie, lecz zakłada on, że faza rozładowania kondensatora trwa dokładnie połowę okresu napięcia zasilającego – co oznaczałoby, że jego ładowanie jest nieskończenie szybkie, bo odbywa się wyłącznie w samym punkcie ekstremum napięcia wejściowego. Można jednak przyjąć, że wzór jest słuszny dla relatywnie niewielkiego napięcia tętnień.
Nie chcę się tutaj zagłębiać się w tajniki dotyczące współczynników tętnień, kształtu i innych, ponieważ zaciemnią one obraz, który powinien pozostać klarowny: chcemy uzyskać możliwie wysoką wartość składowej stałej na wyjściu takiego prostownika z filtrem, najlepiej równą wartości maksymalnej napięcia wejściowego. Oznaczałoby to, że wartość międzyszczytowa składowej zmiennej musiałaby wynosić zero. Z oczywistych przyczyn takie warunki nie są możliwe do spełnienia, bowiem wymagałoby to kondensatora o nieskończenie wielkiej pojemności, który byłby obciążony zerowym prądem. Brzmi mało realistycznie, więc zejdźmy na ziemię.
NAPISZ DO AUTORA
Facebook
Twitter
Linkedin
Kup teraz
