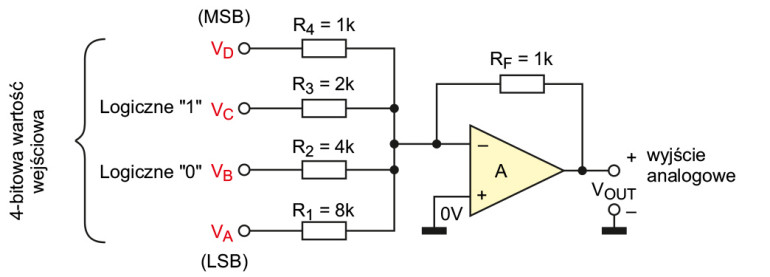
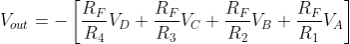Omawianie konwerterów cyfrowo-analogowych zazwyczaj rozpoczyna się od najbardziej intuicyjnego przetwornika binarnie ważonego. Przykład 4-bitowej realizacji takiego układu pokazano na rysunku 1.
Przetwornik binarnie ważony to układ wzmacniacza sumującego napięcia na wejściu odwracającym. Można wykazać, że napięcie wyjściowe VOUT jest równe:
A podstawiając za RF, R1, R2, R3 i R4 wartości z rysunku 1, otrzymamy:
Jeżeli teraz przyjmiemy, że napięcia na wejściach VA…VD przyjmują tylko dwie wartości: 0 V (logiczne zero) lub na przykład +5 V (logiczna jedynka), to otrzymamy na wyjściu analogowym napięcie proporcjonalne do cyfrowego kodu wejściowego.
Opisana topologia może dobrze się sprawdzić w bardzo prostych przetwornikach o kilkubitowej rozdzielczości, natomiast jest zupełnie bezużyteczna w przypadku wielobitowych konstrukcji, koniecznych w wysokiej jakości przetwornikach sygnału audio. W przypadku układu z rysunku 1 rezystancja R1, odpowiadająca najmniej znaczącemu bitowi (LSB), ma wartość 1 kΩ, a R4 – odpowiadająca najbardziej znaczącemu bitowi – ma wartość 8 kΩ, czyli R4=(24)·R1. Przyjmijmy, że mamy taki przetwornik o rozdzielczości 16 bitów, potrzebujemy zatem układu z szesnastoma opornikami. Jeżeli – tak jak na rysunku 1 – oporność R1 będzie równa 1 kΩ, to wartość R16 wyniesie: R16=(216)·R1, czyli: 1 kΩ·65536=65,536 MΩ.
Bardzo trudne jest wykonanie układu dokładnych rezystorów o tak dużej rozpiętości wartości rezystancji, szczególnie w układzie scalonym, który – dla rynku konsumenckiego – musi być stosunkowo tani. Dodatkowo taki układ rezystorów nie będzie stabilny temperaturowo i wraz ze zmianami warunków otoczenia będzie następowała zmiana funkcji przetwarzania, powodująca wprowadzanie błędów do charakterystyki konwertera. Topologia ważonego przetwornika cyfrowo-analogowego, pokazanego na rysunku 1, jest zatem bezużyteczna w wielobitowych układach audio.
Przetwornik o topologii R2-R
Wspomnianej wady układu binarnego ważonego pozbawiona jest topologia drabinki rezystorowej typu R2-R, pokazana na rysunku 2.
Sieć drabinki rezystancyjnej R-2R to długi ciąg równolegle i szeregowo połączonych rezystorów o wartościach R i 2·R. Taki układ jest dużo łatwiej wykonać w technologii scalonej. Sieć działa jako połączone ze sobą, kolejne dzielniki napięcia. Napięcie wyjściowe VOUT zależy wyłącznie od oddziaływania ze sobą napięć wejściowych VA, VB. VC...Vn, a nie bezpośrednio od wartości rezystancji rezystorów drabinki. Napięcia wejściowe mogą zatem przybierać wartości 0 V dla stanu logicznego niskiego lub VIN – dla stanu wysokiego. VIN jest napięciem referencyjnym, nazywanym najczęściej VREF. Analizując sieć rezystorów można wykazać, że napięcie wyjściowe jest równe:
gdzie: n oznacza liczbę wejść cyfrowych przetwornika, czyli jego rozdzielczość bitowa
Rozdzielczość napięciowa przetwornika, czyli zmiana napięcia na wyjściu spowodowana zmianą kodu wejściowego na pozycji najmniej znaczącego bitu, wynosi:
gdzie VIN jest tożsame z napięciem odniesienia VREF.
Przykładowo: dla przetwornika 16-bitowego z napięciem odniesienia równym 5 V rozdzielczość jest równa 5/(216)=5/65536=92 μV. To pokazuje, że nawet przy 16-bitowej rozdzielczości mamy do czynienia z bardzo małymi poziomami, które łatwo jest zdegradować szumem i innymi zakłóceniami toru audio, a tym samym... ograniczyć jego rzeczywistą rozdzielczość.
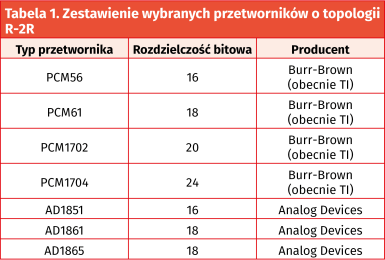
Topologia R-2R jest szeroko stosowana w scalonych przetwornikach audio przeznaczonych dla rynku konsumenckiego. W tabeli 1 pokazano zestawienie wybranych, wielobitowych przetworników audio, opartych na topologii R-2R.
Wszystkie te przetworniki (za wyjątkiem AD1865) mogą konwertować jeden kanał audio, zatem do budowy przetwornika stereofonicznego potrzebne są 2 układy.
Na rysunku 3 pokazano schemat blokowy przetwornika PCM56 firmy Burr Brown. Dane audio, przesyłane szeregowo przez wejścia Clock, LE i Data, są zatrzaskiwane w 16-bitowym rejestrze wejściowym. Po skompletowaniu całego, 16-bitowego słowa dane są przekazywane na przetwornik DAC typu R-2R. Blok Reference dostarcza dokładne i stabilne napięcie referencyjne.
Jak już wspomniałem, możliwe jest wykonanie scalonego przetwornika R-2R wysokiej klasy, jednak wymaga to zaawansowanej technologii łączącej krzemową strukturę układu z rezystorami cienkowarstwowymi. Aby uzyskać dużą dokładność rezystancji, poszczególne elementy w sieci R-2R układu są w procesie produkcyjnym dodatkowo kalibrowane (trymowane) za pomocą lasera. Przykładem zastosowania bardzo wyrafinowanej technologii jest układ PCM1704, który według danych katalogowych uzyskuje rozdzielczość 24-bitową, może próbkować dane z maksymalną częstotliwością fS=96 kHz i charakteryzuje się parametrem THD na poziomie 0,0008%. Zdecydowana większość przetworników wielobitowych cieszy się bardzo dobrą opinią wśród osób ceniących dźwięk na najwyższym poziomie. Jednak mimo tych bardzo dobrych parametrów i opinii, w większości przypadków nie są one produkowane i stosowane w nowych konstrukcjach, a ceny ze starych zapasów osiągają zawrotne wartości. Przyczyną takiego stanu rzeczy jest zapewne bardzo kłopotliwy i – co za tym idzie – kosztowny proces produkcyjny. Ograniczenie stanowi rozdzielczość bitowa, która – za wyjątkiem układów PCM1704 i PCM1702 – wynosi 16 lub 18 bitów, a dodatkowym problemem jest niższa częstotliwość próbkowania. Nie bez znaczenia jest także fakt, że do układów stereofonicznych potrzebujemy 2 przetworników. Ale i to nie wszystko. Kompletne przetworniki potrzebują do pracy trzeciego układu: filtra cyfrowego. Realizuje on proces nadpróbkowania w interpolatorze cyfrowym i cyfrowej filtracji dolnoprzepustowej. Gwoli ścisłości należy wspomnieć, że wśród amatorów DIY na całym świecie istnieje cała rzesza entuzjastów rozwiązania nazywanego NOS DAC, czyli No OverSampling DAC. Przetworniki budowane według tej idei nie mają filtra cyfrowego realizującego nadpróbkowanie, a sygnał PCM jest podawany bezpośrednio na wejście przetworników DAC. Nie stosuje się też dolnoprzepustowych filtrów rekonstruujących. Brak filtra cyfrowego w strukturze przetwornika powoduje, że konieczne są dodatkowe układy logiczne, które dostosowują format I²S do formatu wejściowego przetworników (wymagającego podanie sygnałów Clock, LE i Data).
Brak nadpróbkowania i analogowej rekonstrukcji sygnału wyjściowego ma powodować, że dźwięk po konwersji będzie inny, niż w klasycznych rozwiązaniach – a wg opinii wielu lepszy lub nawet dużo lepszy. Ponieważ jest to artykuł techniczny, nie będziemy nad tym dyskutować – skutki tak wykonanej konwersji możemy zobaczyć, analizując pierwszą część niniejszego opracowania.
Przetwornik DEM (Dynamic Element Matching)
Jak już wspomniałem, choć sieci drabinkowe R2-R pozwalają na zbudowanie konwertera DAC o wysokiej jakości, to ich dobre parametry są okupione trudnościami technologicznymi i – w konsekwencji – relatywnie wysoka ceną. Dlatego szukano przed laty tańszych alternatyw, pozwalających na uzyskanie równie dobrych parametrów, ale mniejszym kosztem.
W 1976 roku Rudy van de Plassche, młody inżynier ds. badań i rozwoju pracujący w Laboratoriach Badawczych Philipsa, publikuje pracę zatytułowaną „Dynamic Element Matching for High-Accuracy Monolithic D/A Converters”, w której proponuje nowatorski, prosty i dokładny konwerter cyfrowo-analogowy o nazwie „Dynamic Element Matching” w skrócie DEM. Ta metoda ta nie wymagała trymowania laserowego rezystorów w trakcie produkcji i mogła być produkowana masowo przy użyciu ówcześnie dostępnej, standardowej technologii bipolarnej.
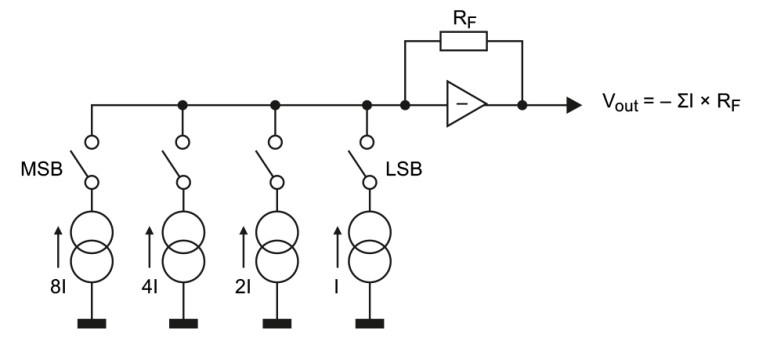
Idea działania jest podobna do ważonego przetwornika binarnego, pokazanego na rysunku 1. Zamiast rezystorów stosuje się jednak źródła prądowe (rysunek 4). Jeżeli bitowi MSB (najstarszemu) przypiszemy źródło w wydajności prądowej I, to kolejnej wadze odpowiadać będzie źródło o wydajności 2/I – i tak dalej, aż do najmłodszego bitu. Oczywiście otrzymamy tu również bardzo dużą rozpiętość wartości prądu, który musi być bardzo precyzyjnie podzielony.
Jeżeli najstarszemu bitowi przetwornika 16-bitowego przypiszemy prąd 2 mA, to w przypadku najmłodszego bitu będzie to natężenie zaledwie 61 nA! Tu musi się pojawić pytanie: jak wygenerować dokładne prądy binarnie ważone (malejące w stosunku 1:2) dla wszystkich naszych bitów danych? Najlepiej dzieląc każdy następny prąd dokładnie na pół. No dobrze, ale jak to zrobić, skoro wiemy, że każdy realny element aktywny lub pasywny wprowadzi jakiś błąd i ten błąd będzie się sumować w każdym kolejnym stopniu podziału?