Jak zbudować własny kalkulator? (działanie, schematy, montaż)

Samodzielna realizacja prostego nawet kalkulatora jest sporym wyzwaniem i pozwala się wiele nauczyć. Dlatego postanowiłem spróbować swoich sił i przy okazji złożyć malutki hołd tym prehistorycznym konstrukcjom.

Jako że kalkulatory nie podzieliły jeszcze losu suwaków logarytmicznych, wydaje mi się, że czytelnik spotkał się już z podobnymi urządzeniami. Prezentowany dalej model potrafi wykonać 5 działań: dodawanie, odejmowanie, mnożenie, dzielenie i pierwiastek kwadratowy. Obliczenia są prowadzone zgodnie z logiką algebraiczną uproszczoną. Oznacza to, że kolejność działań nie jest zachowana. Gdy po kolei naciśniemy klawisze [2][+][3][×][4][=], to na wyświetlaczu zobaczymy wynik 20 (a nie 14). Jest to typowy schemat działania prostych kalkulatorów. Jeżeli część ułamkowa wyniku nie mieści się w całości na wyświetlaczu, jest zaokrąglana w dół, czyli po prostu obcinana.

Opis układu - kalkulator własnej budowy

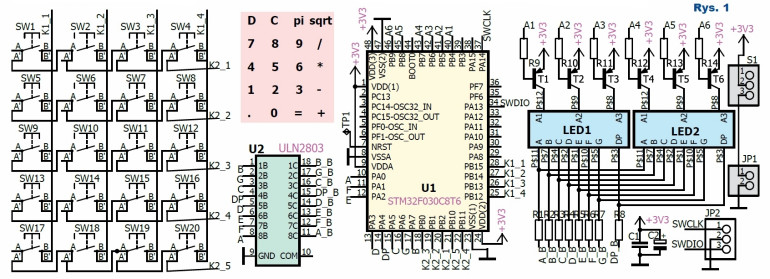
Schemat elektroniczny układu jest przedstawiony na rysunku 1. Cała logika została zrealizowana w mikrokontrolerze STM32F030C8T6 (U1). Jest on wyposażony w 64kB pamięci Flash i 8 kB pamięci RAM. Proponowany program zajmuje niecałe 6kB i wykorzystuje około 300B na dane. Zostaje więc dużo miejsca dla własnych modyfikacji. Na złącze J2 wyprowadzono port SWD pozwalający podłączyć programator. Przyciski SW1-SW20 tworzą klawiaturę. Są one ułożone w cztery kolumny i pięć wierszy podłączonych bezpośrednio do portów wejścia/wyjścia.

Wynik jest wyświetlony na dwóch trzycyfrowych wyświetlaczach LED ze wspólną anodą. Rezystory R1-8 ograniczają prąd, który przez nie płynie. Driver ULN2803 (U2) służy do sterowania katodami. Wyboru obsługiwanego wyświetlacza dokonuje się za pomocą tranzystorów T1–6. Rezystory R9–14 ograniczają prąd ich baz. Układ jest zasilany z dwóch baterii AAA podłączonych do złącza JP1. Oczywiście nie mogło zabraknąć kondensatorów filtrujących C1 i C2. S1 jest przełącznikiem pozwalającym odłączyć dopływ prądu, gdy kalkulator nie jest używany.

Rys.1 Kalkulator własnej budowy - schemat elektroniczny układu

Program można znaleźć w materiałach dodatkowych oraz w repozytorium [2]. W głównym folderze znajdziemy kod startowy (startup.S), skrypt linkera (linker.ld) oraz Makefile zawierający reguły kompilacji. Kod źródłowy został rozlokowany w podfolderach. Folder CMSIS zawiera definicję i adresy rejestrów mikrokontrolera. Zostały one stworzone przez firmę ARM oraz STMicroelectronics i są udostępniane za darmo. Program kalkulatora został podzielony na dwa foldery: inc zawiera nagłówki, a src kod źródłowy. Nietypowy jest natomiast folder tests, który zawiera tak zwane testy jednostkowe.

Pliki ui.h i ui.c zawierają kod odpowiedzialny za obsługę interfejsu użytkownika (ang. user interface), na który składa się klawiatura oraz wyświetlacze siedmiosegmentowe. Aby zaoszczędzić piny procesora, w danej chwili świeci się tylko jedna cyfra. Przełączanie odbywa się w przerwaniu od licznika (ang. timer) 14, które jest wywoływane 500 razy w ciągu sekundy.

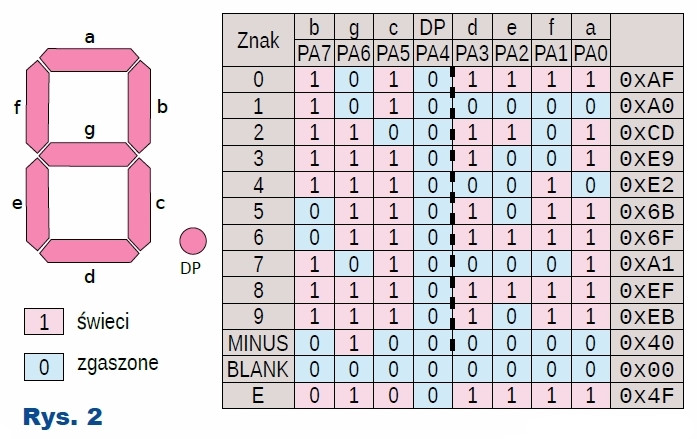
Ponieważ cyfr jest sześć, oznacza to, że wyświetlacz jest odświeżany z częstotliwością około 80 Hz, dzięki czemu miganie nie jest widoczne. Dla wyświetlacza zdefiniowano 13 różnych znaków, których „kody” są pokazane na rysunku 2. Są one zdefiniowane w tablicy NUM. Ponieważ do sterowania wykorzystano układ ULN2803, dioda świeci się, gdy na pinie mikrokontrolera panuje stan wysoki. Aktualnie wyświetlana wartość jest przechowywana w tablicy data i może być zmieniana za pomocą funkcji set_digits().

Rys.2 Znaki kalkulatora i ich kody

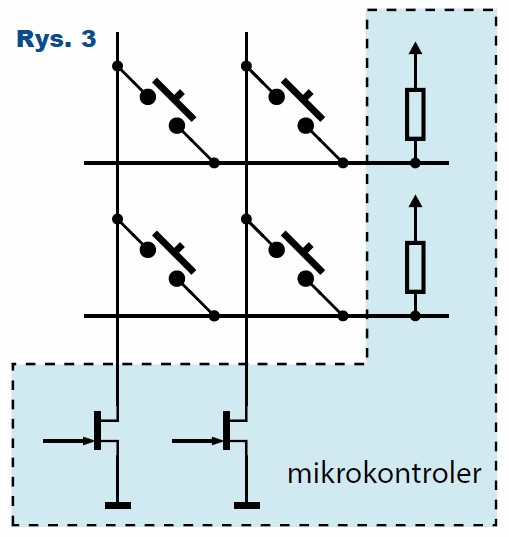
Klawiatura także jest multipleksowana. W jednym kroku odczytywany jest stan pięciu klawiszy z aktywnej kolumny. Dzięki temu, że konfiguracja portów jest bardzo elastyczna, nie są potrzebne żadne dodatkowe elementy. Jak pokazano na rysunku 3, wyjścia sterujące kolumnami pracują w trybie otwarty dren (który działa tak samo jak otwarty kolektor).

Dzięki temu kolumna może być albo ściągnięta do masy (aktywna), albo „wisieć w powietrzu” (nieaktywna). Wiersze pracują jako wejścia dodatkowo są podciągnięte za pomocą wewnętrznego rezystora do plusa zasilania. Naciśnięcie przycisku należącego do aktywnej kolumny spowoduje wymuszenie stanu niskiego. Aby wyeliminować drgania styków, każdy z przycisków jest obsługiwany przez osobną maszynę stanów. Zapewnia ona, że zmiana stanu przycisku następuje dopiero, jeżeli 5 kolejnych odczytów będzie identycznych. Gdy zostanie wykryte naciśnięcie któregoś z klawiszy, nastąpi ustawienie flagi, która jest sprawdzana w programie głównym.

Rys.3 Wyjścia sterujące kolumnami pracują w trybie otwarty dren

Logika kalkulatora znajduje się w plikach calc (.c i .h). Ale najpierw zastanówmy się, jak możemy ją przedstawić. Tu znów z pomocą przychodzi koncepcja maszyny stanów. Zakłada ona, że kolejny stan kalkulatora możemy wyznaczyć na podstawie stanu obecnego oraz wejścia. Wejściem w naszym przypadku jest fakt naciśnięcia klawisza. Możemy to zapisać:

stant+1 = funkcja_przejścia(stant, naciśnięty_przycisk)

Musimy jednak ustalić, w jaki sposób opisać aktualny stan. Ja wykorzystałem do tego strukturę calc, przedstawioną na poniższym listingu. Składa się z ośmiu pól ułożonych w kolejności od największego do najmniejszego. Taki układ zapewnia najlepsze wykorzystanie dostępnej pamięci.

1 struct calc {
2 int64_t memory;
3 int64_t display;
4 enum calc_state state;
5 enum calc_error error;
6 enum fp_sign sign;
7 enum button operand;
8 int8_t dot_position;
9 int8_t digits;
10 };

Zmienna display przechowuje wartość aktualnie wyświetlaną na ekranie kalkulatora, reprezentowaną w systemie stałoprzecinkowym bez znaku. Ponieważ kalkulator może wyświetlić 6 cyfr, oznacza to, że po przecinku znajdzie się maksymalnie pięć pozycji. Aby to osiągnąć, wartość przed wpisaniem do zmiennej jest mnożona przez 10⁵, czyli 100 000. Osobno przechowywana jest informacja o znaku (sign) i liczbie miejsc po przecinku (dot_position). Jest to niezbędne, ponieważ w momencie wprowadzania cyfry nie da się tych informacji przechowywać w zmiennej display. Z punktu widzenia matematyki liczby 0, –0, czy –0.0 są wszystkie równe 0. Natomiast w przypadku kalkulatora są to kolejne stany, przez które przechodzi, gdy użytkownik wpisuje na przykład liczbę –0.01 i muszą one być rozróżnialne.

Rys.4 Zmienne

Dla ułatwienia dodatkowo zmienna digits przechowuje liczbę wykorzystanych pól wyświetlacza, dzięki czemu łatwiej stwierdzić, czy użytkownik może dodać kolejny znak. Zmienna state może przyjmować dwie wartości: oczekiwanie na wprowadzenie nowej liczby albo kontynuację wpisywania starej, error natomiast przechowuje informację o błędzie.

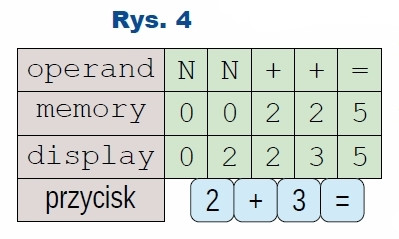
Może przyjąć cztery wartości: brak błędu, przepełnienie, dzielenie przez zero oraz wyciąganie pierwiastka z liczby ujemnej (obecna wersja oprogramowania nie obsługuje liczb urojonych). Kolejne działanie do wykonania jest przechowywane w zmiennej operand. Zmienna memory przechowuje poprzednią wprowadzoną liczbę albo wynik poprzedniej operacji, który będzie wykorzystany przy obliczaniu kolejnej. Ich działanie ilustruje rysunek 4.

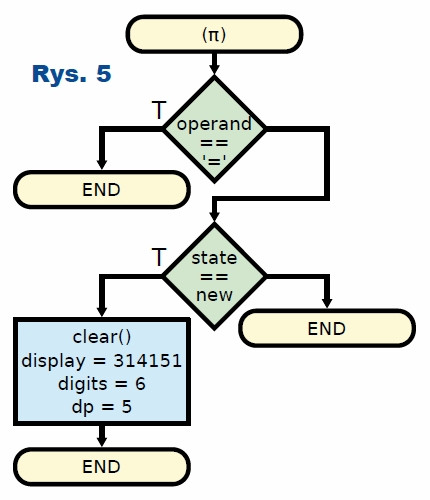
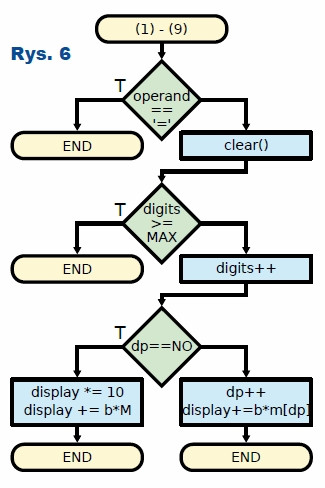
Zastanówmy się teraz, w jaki sposób stan kalkulatora powinien się zmieniać po naciśnięciu różnych przycisków. Zacznijmy od stosunkowo prostego przypadku: π. Algorytm został przedstawiony na rysunku 5. Jeżeli automat czeka na rozpoczęcie wpisywania nowej liczby, ustawiane są odpowiednie wartości. W przeciwnym razie stan się nie zmienia. Bardziej złożona jest obsługa klawiszy z cyframi od 1 do 9 (rysunek 6). Jeżeli aktualnie jest wczytywana liczba oraz na ekranie jest jeszcze miejsce, liczba zajętych cyfr jest zwiększana.

Natomiast samo dopisanie liczby może przebiec w dwóch wariantach. Dla części całkowitej najpierw następuje przesunięcie obecnie wprowadzonych cyfr w prawo, a następnie dodanie nowej cyfry, pomnożonej razy 10⁵. W przypadku części ułamkowej nie musimy przesuwać starej wartości, natomiast nową cyfrę umieszczamy na odpowiedniej pozycji poprzez pomnożenie jej razy 10^{5-miejsce_ po_przecinku}. Wartość ta jest odczytywana z tabeli.

Rys.5 Własny kalkulator - algorytm π

Rys.6 Algorytm obsługi klawiszy z cyframi od 1 do 9

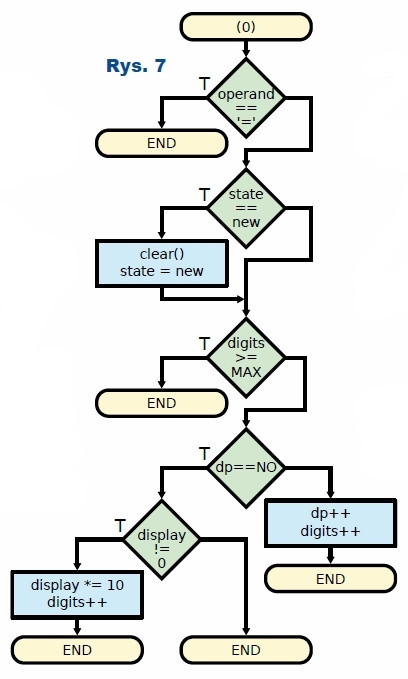
Jak pokazuje rysunek 7, cyfra 0 jest przypadkiem szczególnym, ponieważ od razu wycinane są nieznaczące zera, dodawane na początku liczby. Uwzględniane muszą być natomiast te, które są dopisywane po przecinku, ponieważ w przeciwnym razie nie dałoby się na przykład wpisać liczby 0.01.

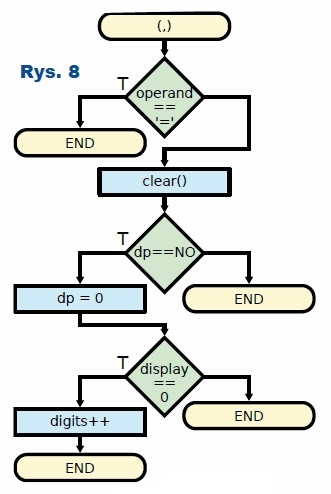
Na rysunku 8 przedstawiona jest obsługa przycisku kropki, która oddziela część całkowitą od części ułamkowej. Jeżeli aktualnie wpisywana jest nowa liczba, następuje sprawdzenie, czy części ułamkowa jest już obecna. Jeżeli tak, przycisk jest ignorowany, a stan nie ulega zmianie. W przeciwnym przypadku dot_position przyjmuje wartość 0, co spowoduje, że kolejne cyfry będą już interpretowane jako część ułamkowa. Należy także sprawdzić, czy na wyświetlaczu jest wyświetlane 0. Jeżeli tak, to z cyfry nieznaczącej zmieni się ono w cyfrę znaczącą, przez co należy zwiększyć liczbę zajętych wyświetlaczy.

Rys.7 Algorytm obsługi cyfry '0'

Rys.8 Algorytm obsługi przycisku kropki

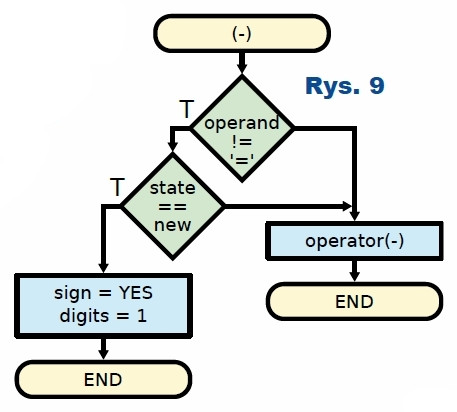
Klawisz [–] ma dwie funkcje. Jeżeli jest naciśnięty na początku wprowadzania liczby, powoduje, że będzie ona traktowana jako ujemna. Jak pokazuje rysunek 9, spowoduje to zwiększenie liczby wykorzystanych wyświetlaczy oraz przypisanie zmiennej sign wartości 1. W przeciwnym przypadku jest on traktowany jako dwuargumentowy operator odejmowania i jego obsługę przejmuje funkcja operator, która zostanie omówiona dalej.

Rys.9 Algorytm obsługi przycisku odejmowania

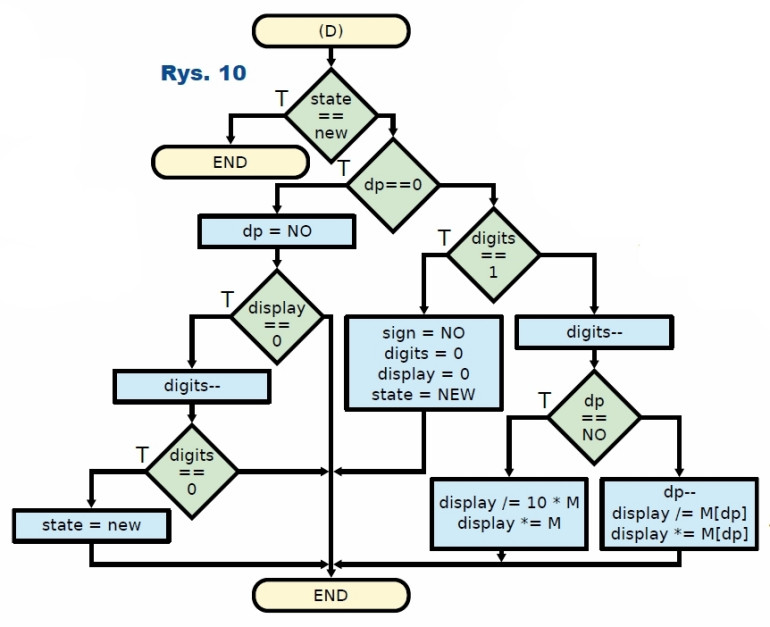
Ostatnim elementem wpisywania liczby jest klawisz D (kasować, od ang. delete). Jak można zobaczyć na rysunku 10, jego działanie jest najbardziej rozbudowane ze wszystkich dotąd omówionych. Na podstawie obecnego stanu kalkulatora cofa go do takiego stanu, w jakim był przed naciśnięciem poprzedniego przycisku. Wyjątek stanowi π, które zostaje potraktowane w taki sposób, jakby użytkownik sam wpisał kolejne jej cyfry. Takie działanie wydaje mi się jednak bardziej intuicyjne.

Rys.10 Algorytm obsługi klawisza 'delete'

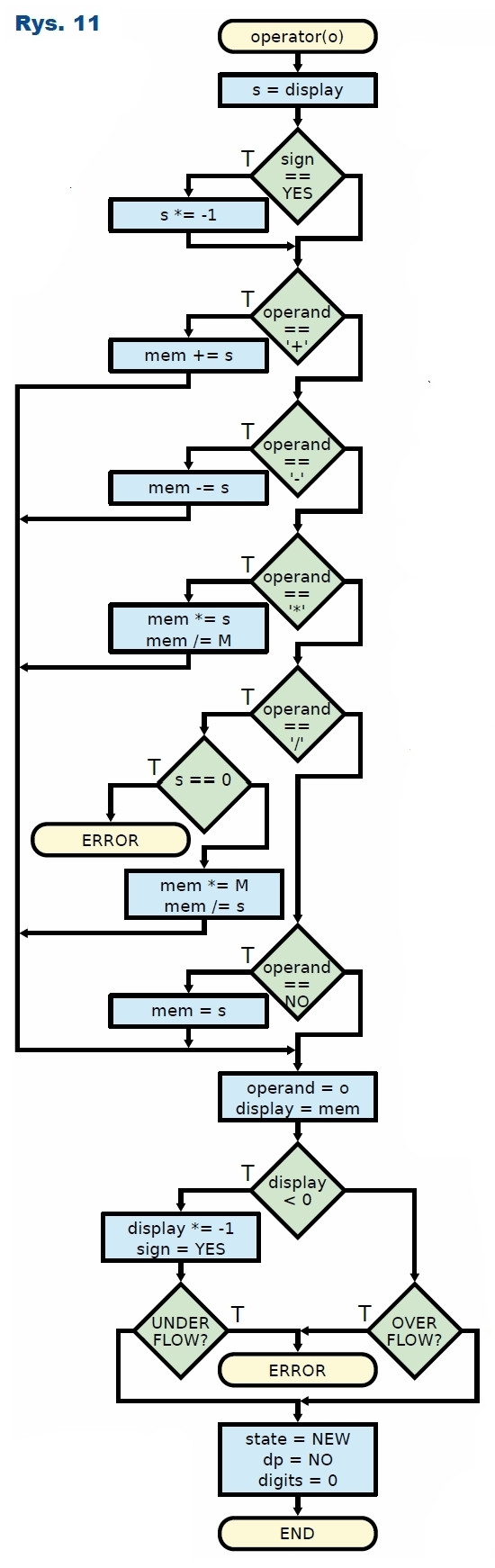
Teraz możemy przejść do części odpowiedzialnej za wykonywanie obliczeń. Dodawanie, odejmowanie, mnożenie, dzielenie oraz znak równości są obsługiwane przez funkcję przedstawioną na rysunku 11. Na początku kopiuje on wartość ze zmiennej display i uzupełnia ją o znak. Następnie jest wykonywana operacja arytmetyczna, ale nie ta, która wywołała obliczenia, lecz zapisana poprzednio.

Rys.11 Dodawanie, odejmowanie, mnożenie, dzielenie oraz znak równości (algorytmy)

Wynik jest umieszczany w zmiennej memory. Dodawanie i odejmowanie jest intuicyjne. Wyjaśnienia wymaga mnożenie i dzielenie. Operacje te zmieniają liczbę znaków po przecinku, dlatego niezbędne jest dodatkowe przesunięcie znaku poprzez dzielenie/mnożenie przez mnożnik M równy 10⁵. Na końcu następuje wyświetlenie wyniku oraz oczekiwanie na wpisanie nowej liczby.

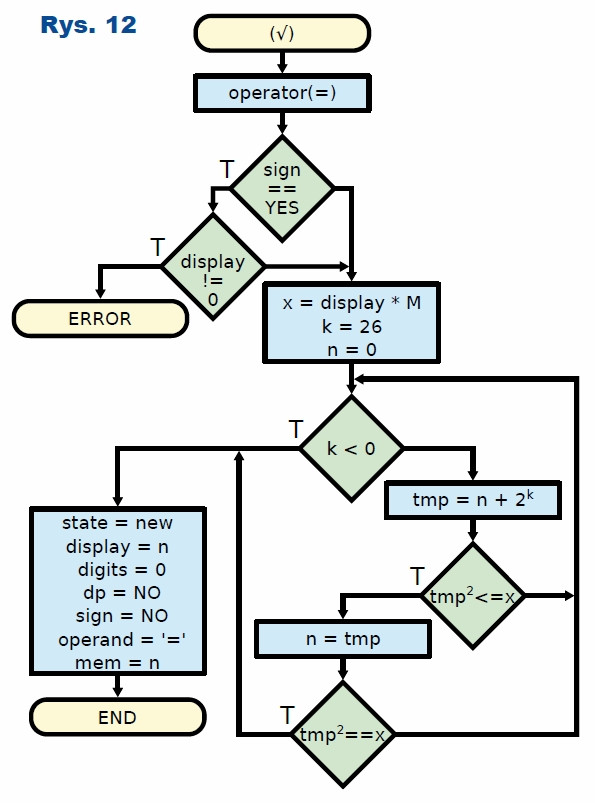
Pierwiastek traktowany jest osobno. Algorytm jego obliczania przedstawia rysunek 12. Najpierw następuje obliczenie oczekującego działania poprzez wywołanie funkcji operator dla działania [=]. Następnie, ponieważ liczba jest zapisana w postaci x×10⁵ i chcemy, aby wynik miał tę samą postać, musimy przemnożyć wejściową wartość przez 10⁵.

Rys.12 Algorytm obliczania pierwiastka

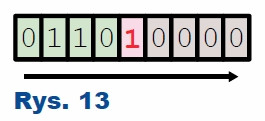
Do obliczeń wykorzystano wyszukiwanie binarne. W każdym kroku algorytmu sprawdzamy, czy kolejny bit liczby powinien mieć wartość 0, czy 1. Jak przedstawiono na rysunku 13, zaczynamy od najbardziej znaczącego i przesuwamy się w prawo. Kolorem zielonym zaznaczono te bity, których wartość została ustalona w poprzednim kroku. Aktualnie sprawdzany bit ma kolor czerwony. Algorytm ustawia go na 1 i liczy kwadrat tak powstałej liczby.

Rys.13 Wyszukiwanie binarne

Jeżeli uzyskany wynik jest równy pierwiastkowanej liczbie, oznacza to, że znaleźliśmy wynik. W przeciwnym razie musimy przejść do kolejnego kroku. Testowany bit pozostawiamy ustawiony, jeżeli uzyskany wynik był za mały. Największa liczba, jaką będziemy pierwiastkować, może być równa 9 9 9 9 9 9 × 1 0 ^{1 0} , czyli mniejsza od 10¹⁶. Oznacza to, że wynik nie będzie większy niż 10⁸, co jest mniejsze niż 2²⁷. Wiemy więc, że bity od 27 w górę będą zawsze miały wartość równą 0. Właśnie dlatego na początku zmienna k jest równa 26.

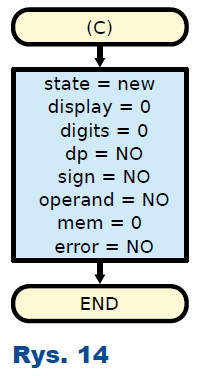
Ostatnim przyciskiem jest C – kasowanie. Jak pokazuje rysunek 14, sprowadza on stan automatu do początkowego. Jest to jedyny przycisk pozwalający na wyjście z obsługi błędów.

Rys.14 Algorytm przycisku 'C' (kasowanie)

Funkcja calc_to_digit przyjmuje strukturę opisującą stan kalkulatora i przetwarza ją na stan sześciu wyświetlaczy. Na początku sprawdza, czy wyświetlić błąd i w razie potrzeby powoduje wyświetlenie odpowiedniego komunikatu. Jeżeli nie, to przechodzi do rozkładu liczby na poszczególne cyfry. Najpierw sprawdzany jest znak, następnie część całkowita, a na końcu wolne pola wyświetlacza zapełniane są częścią ułamkową.

Funkcja main znajduje się w pliku main.c. Najpierw następuje w niej konfiguracja portów wejścia, wyjścia, licznika oraz przerwań. Następnie w pętli głównej sprawdzana jest flaga sygnalizująca naciśnięcie przycisku. Gdy to nastąpi, wykonywana jest funkcja przejścia automatu stanu i aktualizowana jest wyświetlana liczba.

Na końcu pliku calc.c, oddzielone dyrektywą #ifdef TESTS, znajdują się testy jednostkowe. Zostały one stworzone w oparciu o framework Tinytest [3]. Pozwalają „przeklikać” poszczególne funkcje kalkulatora bez uruchamiania programu na mikrokontrolerze. Program jest skompilowany i uruchomiony na komputerze PC, a kolejne stany automatu są porównywane ze zdefiniowanymi przeze mnie ręcznie wartościami umieszczonymi w plikach calc_test_*.h. Testy pisałem równolegle z dodawaniem kolejnych funkcjonalności. Dzięki temu w czasie implementacji kolejnych elementów mogłem na bieżąco sprawdzać, czy działają one zgodnie z oczekiwaniem oraz czy nie psują one starych (ładniej mówiąc, czy nie wprowadzają regresji).

Można je uruchomić w systemie Linux albo w systemie Windows, korzystając z Podsystemu Windows dla systemu Linux. Kod możemy pobrać z materiałów dodatkowych albo z repozytorium za pomocą polecenia:

git clone git@gitlab.com:kozik/calculator.git

Aby uruchomić testy, należy wejść do folderu tests i rozpocząć kompilację:

make
gcc -c -o obj/calc.o ../src/calc.c
-I../inc -D TESTS
gcc -c -o tinytest.o tinytest.c -I../
inc -D TESTS
gcc -o tinytest tinytest.o obj/calc.o
A następnie uruchomić program:
./tinytest
.....
OK: 5

W przypadku gdy test się nie powiedzie, zamiast kropki wyświetlony zostanie x oraz pojawi się stosowna informacja.

Montaż i uruchomienie własnego kalkulatora  

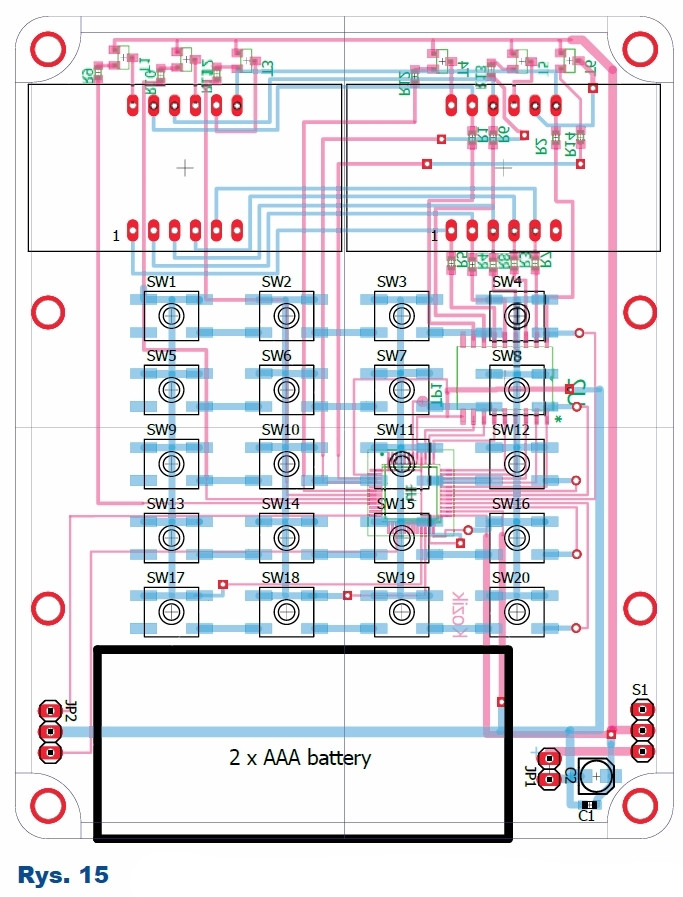
Projekt dwustronnej płytki drukowanej przedstawia rysunek 15. Montaż najlepiej rozpocząć od części najmniejszych do największych. Przed rozpoczęciem lutowania elementów smd warto zaopatrzyć się w pincetę, plecionkę lutowniczą oraz kalafonię. Po montażu należy za pomocą testera zwarcia sprawdzić, czy nie powstały zwarcia. Zlutowany układ przedstawiają fotografia 1 (góra) i fotografia 2 (dół).

Rys.15 Własny kalkulator - projekt dwustronnej płytki drukowanej

Fot.1 Kalkulator własnej budowy - zlutowany układ (góra)

Fot.2 Kalkulator własnej budowy - zlutowany układ (dół)

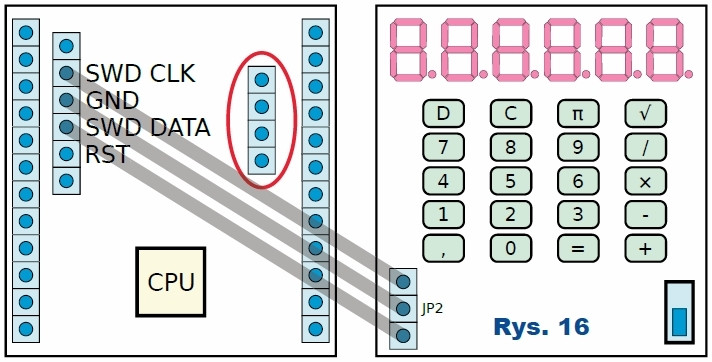
Skompilowany, gotowy do wgrania program znajduje się w pliku main.bin w materiałach dodatkowych. Jeżeli czytelnik chciałby wprowadzić własne modyfikacje do kodu do kompilacji, może wykorzystać skrypt Makefile. Konieczna będzie modyfikacja zmiennej GNUDIR tak, żeby zawierała ścieżkę do folderu z narzędziami GNU dla procesorów ARM. Jako programator można wykorzystać zestawy Discovery albo Nucleo. Sposób podłączenia jest pokazany na rysunku 16. Należy pamiętać o rozwarciu zworek zaznaczonych czerwoną elipsą.

Rys.16 Sposób podłączenia programatora

Rys.17 Nadruk na przyciski kalkulatora

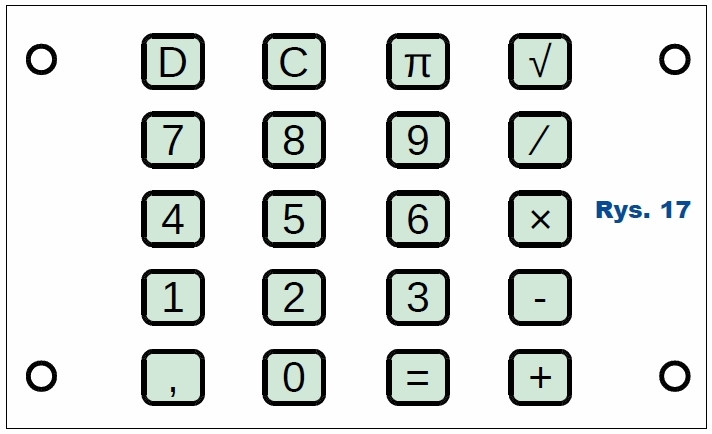
Aby ułatwić korzystanie z kalkulatora, na przyciski warto zamontować nadruk przedstawiony na rysunku 17 (oraz w pliku calc_key.odg). W moim modelu został on wydrukowany na folii rzutnikowej, a następnie zalaminowany w celu zwiększenia sztywności. Do płytki został zamocowany za pomocą czterech śrub o średnicy 3 i długości 10mm. Jako dystanse pomiędzy wydrukiem, a PCB wykorzystano nakrętki o średnicy 5 mm. Niestety wydruk na przezroczystej folii był mało widoczny, dlatego konieczne okazało się podłożenie pod nią kartki białego papieru.

Rys.18 Podstawka do kalkulatora zrobiona z plexi - projekt

Fot.3 Podstawka do kalkulatora zrobiona z plexi

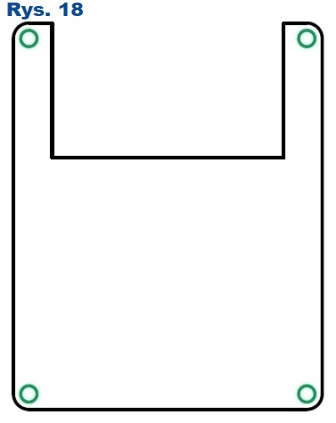
Rysunek 18 i fotografia 3 (calc_podstawka.dxf) przedstawiają podstawkę, którą można wyciąć laserem z 4mm plexi. Znajduje się w niej miejsce na koszyk z bateriami AAA, który przyklejamy do PCB klejem na gorąco. Aby nie wystawał on poza obudowę, jako dystans konieczne było użycie aż 4 dodatkowych nakrętek przy każdej ze śrub. Dzięki niej kalkulator może stabilnie leżeć na biurku. Proces jej montażu przedstawia film [4], a gotowy efekt widać na fotografii tytułowej.

[1] Roberts, Ed (November 1971). „Electronic desk calculator you can build”. Popular Electronics. Vol. 35 no. 5. pp. 27–32. https:// www.americanradiohistory.com/ Archive-Poptronics/70s/1971/Poptronics- 1971-11.pdf

[2] gitlab.com/kozik/calculator

[3] https://github.com/ccosmin/tinytest

[4] https://youtu.be/OonAoCeoLJY