Zaloguj się
Wszystkie
10 września 2021
718
Nie przedłużając chodzi o:
n dwuwejściowych bramek XNOR o wyjściach dołączonych do n-wejściowej bramki AND,
jeżeli n > 1. W przeciwnym razie (dla n = 1) jest to pojedyncza bramka XNOR z dwoma wejściami,
bądź równoważnie:
n dwuwejściowych bramek XOR o wyjściach dołączonych do n-wejściowej bramki NOR,
jeżeli n > 1. W innym razie (n = 1) jest to pojedyncza bramka XNOR z dwoma wejściami.
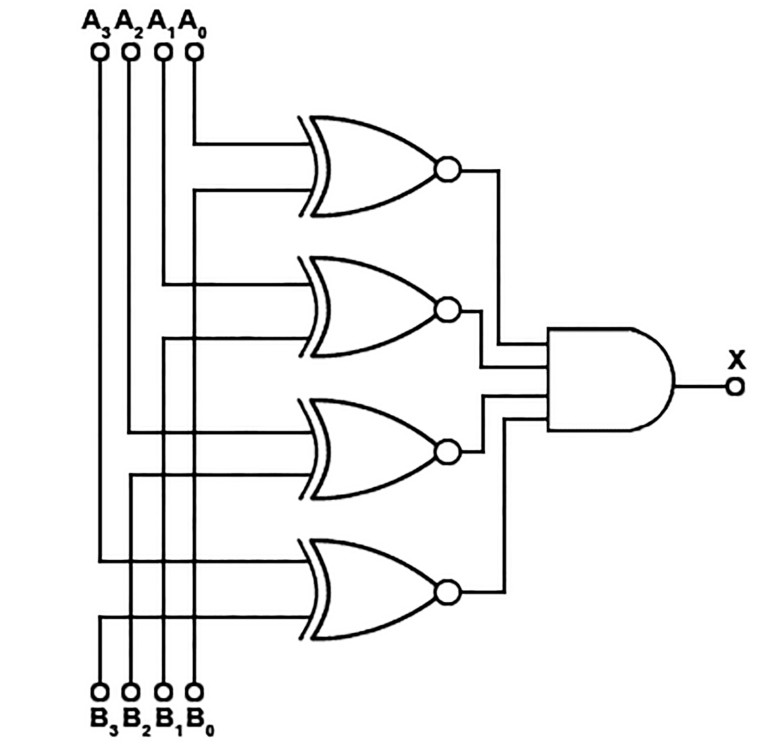
Razem n+1 bramek logicznych w pierwszym przypadku bądź jedna w drugim - i nic więcej! Ot prosty to układ - poniżej jego przykład dla n = 4 (wziąwszy pod uwagę pierwszą wersję reguły).
Oczywiście można dojść do niego wspomnianą w tytule siatką, lecz wtedy trzeba jeszcze dokonać dodatkowego przekształcenia, którym jest pogrupowanie w nawiasy składników otrzymanej funkcji logicznej (lub ściślej: formy boolowskiej). W praktyce rzecz to prosta, lecz nie każdy o niej pamięta, zwłaszcza osoba początkująca. Dopiero po jej zastosowaniu widać jak na dłoni to co na początku zostało wskazane.
Fajnie, tylko po co dochodzić do tego samego wiele razy? Lepiej poprzestać na tym co jest uzyskiwane - stąd ostatnie zdanie w tytule. Taka to zagwozdka - tak to się „porównuje”!
Facebook
Twitter
Linkedin
Kup teraz
